


The Geomag construction game is another way to explore the world of polyhedra; here is a nice example.
Here are the characteristics of the semi-regular polyhedra of the first kind (for their duals we have just to exchange v and f):
| s | a | f | f3 | f4 | f5 | f6 | f8 | f10 | fn | dual polyhedron (face) | ||
| truncated tetrahedron | 12 | 18 | 8 | 4 | - | - | 4 | - | - | - | triakis-tetrahedron (isosceles triangle) | |
| truncated cube | 24 | 36 | 14 | 8 | - | - | - | 6 | - | - | triakis-octahedron (isosceles triangle) | |
| truncated octahedron | 24 | 36 | 14 | - | 6 | - | 8 | - | - | - | tetrakis-hexahedron (isosceles triangle) | |
| cuboctahedron | 12 | 24 | 14 | 8 | 6 | - | - | - | - | - | rhombic dodecahedron (rhombus) | |
| small rhombicuboctahedron | 24 | 48 | 26 | 8 | 18 | - | - | - | - | - | deltoidal icositetrahedron(kite) | |
| great rhombicuboctahedron | 48 | 72 | 26 | - | 12 | - | 8 | 6 | - | - | disdyakis-dodecahedron (triangle) | |
| snub cube | 24 | 60 | 38 | 32 | 6 | - | - | - | - | - | pentagonal icositetrahedron (pentagon) | |
| truncated dodecahedron | 60 | 90 | 32 | 20 | - | - | - | - | 12 | - | triakis-dodecahedron (isosceles triangle) | |
| truncated icosahedron | 60 | 90 | 32 | - | - | 12 | 20 | - | - | - | pentakis-dodecahedron (isosceles triangle) | |
| icosidodecahedron | 30 | 60 | 32 | 20 | - | 12 | - | - | - | - | rhombic triacontahedron (rhombus) | |
| small rhombicosidodecahedron | 60 | 120 | 62 | 20 | 30 | 12 | - | - | - | - | deltoidal hexecontahedron (kite) | |
| great rhombicosidodecahedron | 120 | 180 | 62 | - | 30 | - | 20 | - | 12 | - | disdyakis-triacontahedron (triangle) | |
| snub dodecahedron | 60 | 150 | 92 | 80 | - | 12 | - | - | - | - | pentagonal hexecontahedron (pentagon) | |
| regular prisms (order n ≥ 3) | 2n | 3n | n+2 | - | n | - | - | - | - | 2 | regular diamonds (isosceles triangle) | |
| regular antiprisms (order n ≥ 3) | 2n | 4n | 2n+2 | 2n | - | - | - | - | - | 2 | regular antidiamonds (kite) |
In "rhombicuboctahedron" the prefix "rhombi" points out that 12 square faces belong to the faces of a rhombic dodecahedron (dual of the cuboctahedron).
Likewise the 30 square faces of the "rhombicosidodecahedra" belong to the faces of a rhombic triacontahedron (dual of the icosidodecahedron).
The great rhombicuboctahedron is also the truncated cuboctahedron; likewise the great rhombicosidodecahedron is the truncated icosidodecahedron.
Generalization to non convex polyhedra: f + v = e + 2 - 2t where t is the number of tunnels of the polyhedron (its genus).
 |
 |
 |
|
Nice polyhedra can be built in many different ways: glued wood, welded copper wire, origami...
The Geomag construction game is another way to explore the world of polyhedra; here is a nice example. | ||
| examples : | cube : 8[2π-3(π/2)] = 4π
regular tetrahedron: 4[2π-3(π/3)] = 4π regular dodecahedron: 20[360°-3x108°] = 720° |
cuboctahedron: 12[2π-2(π/2+π/3)] = 4π
regular pentagonal pyramid: 5[360°-(108°+2x60°)]+(360°-5x60°) = 720° rhombic dodecahedron: 6[360°-4α]+8[360°-3(180°-α)] = 720° α=35.265...° |
Remark about the sum of all the face angles: (Σαij)/2π = a-f = s-2 | ||
| examples : | cube : 8[3(π/2)]/2π = 6 12-6 = 8-2 = 6
regular tetrahedron: 4[3(π/3)]/2π = 2 6-4 = 4-2 = 2 regular dodecahedron: 20[3x108°]/360° = 18 30-12 = 20-2 = 18 |
cuboctahedron: 12[2(π/2+π/3)]/2π = 10 24-14 = 12-2 = 10
regular pentagonal pyramid: [5(108°+2x60°)+5x60°]/360° = 4 10-6 = 6-2 = 4 rhombic dodecahedron: [6x4α+8x3(180°-α)]/360° = 12 24-12 = 14-2 = 12 |
Convexity is a quite natural notion. Without giving an explicit definition it's easy to recognize a convex polyhedron: all its "real diagonals" (segments joining two vertices which don't belong to the same face) are inside.
Minkowski's condition: Let u1, u2, ... uk be unit vectors that span the space, and a1, a2, ... , ak positive numbers. Then there exists a convex polyhedron (unique up to translation) having facet unit normals u1, u2, ... uk and corresponding facet areas a1, a2, ... , ak if and only if a1 u1 + ... + ak uk = 0 (condition for convex polytopes)
Of course we can be interested in a specific category of convex polyhedra, for instance:
• the polyhedra with regular faces: we know those discovered by Plato and Archimedes, the prisms and antiprisms;
the other are the 92 Johnson's solids (pyramids, diamonds, cupolas... assemblages of the previous),
• the different types of hexahedra, less easy to find as the tetrahedra (which have all four triangular faces) or the pentahedra (whose two types are the quadrilateral pyramids and the "roofs" formed by three quadrilaterals and two triangles),
• the deltahedra whose faces are all equilateral triangles,
• the polyhedra with a given number of faces,
• the pyramids which allow to produce jigsaws,
• the tectohedra which are obtained by successive cuttings of tetrahedra,
• the Waterman's polyhedra whose vertices are centers of spheres in a cubic close packing,
• the zonohedra whose faces have all a center of symmetry,
• the zonish polyhedra with "zones" of parallelograms,
• the rhombic polyhedra whose faces are all rhombi,
• the polyhedra with regular faces and golden rhombi,
• the polyhedra with regular faces and 1:1:1:2 isosceles trapezoids,
• the polyhedra with regular faces and specific rhombi (SR2 or golden rhombi),
• the spherical polyhedra (domes),
• the Goldberg's polyhedra,
• the 144 polyhedra which we get by truncations of edges of the cube,
• the symmetrohedra: convex polyhedra with "not much" types of faces, among them "many" regular ones (pdf document),
• simplest examples of canonical polyhedra with one of the 17 types of symmetry,
• . . .
Many other examples have interesting properties: the alveolus of a honeycomb, the crystals, the fullerenes (molecules of carbon), the cut gems . . .

Polyhedra with only pentagonal and hexagonal faces have always twelve pentagonal faces.
The fullerenes have such structures, for example the C60 (truncated icosahedron with 20 hexagonal faces) and the C80 (truncated rhombic triacontahedron with 30 non regular hexagonal faces).
Fedorov's parallelohedra verify three conditions: the faces are two by two opposite and parallel, each edge belongs to a set of parallel edges (four or six edges), and they fill the space using only translations. There are only five, with their affine transformations: the truncated octahedron, the elongated rhombic dodecahedron, the rhombic dodecahedron, the hexagonal prism (not necessarily regular or right) and the cube (thus also all the parallelepipeds); starting with the 6 set of 6 parallel edges of the truncated octahedron, we suppress, by steps, sets of parallel edges to get the others and to end up at the three set of four edges of the cube.
The convex hull (or convex envelope) of a polyhedron P is the unique smallest convex polyhedron which contains P.
|
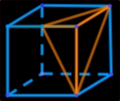
• cuts in a cube (The Mathematical Gazette)
In a cube of side 1 we cut all the "cube corner" tetrahedra of the type indicated in the drawing (if we take the cut as base, the three side edges are two edges and a half edge of the cube). Describe and draw the remaining polyhedron, then calculate its volume. |
 |
| references: |
• Twenty Proofs of Euler's Formula on "The Geometry Junkyard"
• If you wish to handle, modify the appearance, color according to your taste, and print the templates of 147 convex polyhedra, then POLY is the program you need! • With STELLA you may access an infinity of polyhedra (convex or not) and create new ones. A "must" for those who want explore deeper the polyhedra world! • A nice set of 30 convex wooden polyhedra. • Some results about convex polyhedra by Gérard P. Michon. |
home page
 |
convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects | April 1999 updated 27/05-2023 |