Schlegel diagrams
fundamental theorem
Schlegel diagrams are planar graphs (graphs that can be drawn in the plan without edges crossing) associated with polyhedra: the nodes and lines of the graph correspond to the vertices and edges of the polyhedron.
Theorem: Any 3-connected graph can be realized as a convex polyhedron, and a graph associated with a polyhedron is 3-connected.
A simple description of 3-connectedness is: any pair of vertices is connected by three different paths; this is equivalent to the fact that any two vertices can be removed, and all the edges using them, without disturbing the connectedness of the graph.
| An elementary way to draw the Schlegel diagram of a polyhedron is to "project" the polyhedron's skeleton on one of its faces (the nodes corresponding to the vertices which not belong to that face must lie inside the face). |
 |
a few examples
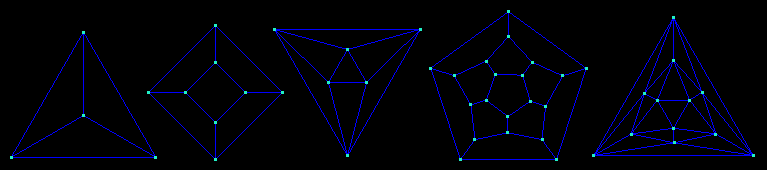
The Schlegel diagrams of the five platonical polyhedra (tetrahedron, cube, octahedron, dodecahedron and icosahedron):
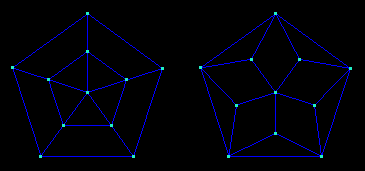
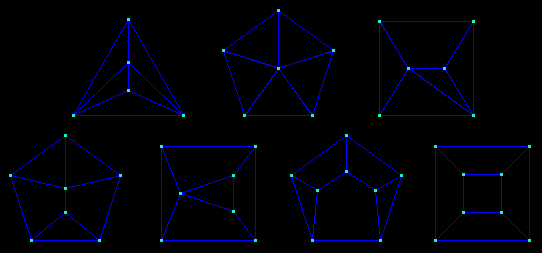
The diagrams of the two types of pentahedra (pyramids and "roofs"):
The diagrams of the seven types of convex hexahedra:
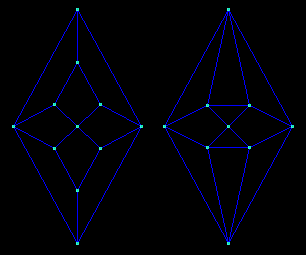
The hermaphrodites are assemblings of a half prism and a half diamond.
The antihermaphrodites are assemblings of a half antiprism and a half antidiamond.
Here are the diagrams of the pentagonal forms of this two polyhedra whose canonical forms are self-dual (11 faces and 11 vertices).
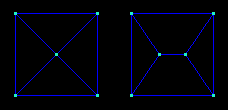
Diagrams of two curious polyhedra: the simplest with an odd number of n-faces (9 quadrilaterals) and a topological dual.
a proof of Euler's formula: f+v = e+2
We move from the polyhedron to its Schlegel diagram by removing a face: the formula becomes polygons + vertices = sides + 1
Then we apply to the diagram transformations which don't modify this relation p+v=s+1 :
• we triangulate all the polygons using diagonals: for each diagonal we add one side and one polygon
• we suppress the triangles starting at the border of the diagram:
- if only one triangle's side belongs to the diagram border we suppress this side and the triangle,
- if two sides belong to the border we suppress these two sides, their common vertex and the triangle.
When only one triangle is left we have 1+3=3+1 which corresponds to p+v=s+1 for all diagrams, and to f+v=e+2 for the polyhedron.

On this example (hexahedron with 6+8=12+2) we have successively 5+8=12+1, 9+8=16+1, 8+8=15+1, 7+8=14+1, 6+7=12+1 ... and finally 1+3=3+1.