the seven types of convex hexahedra

H 1 H 2 H 3 H 4 H 5 J 6 H 7 hexaèdres

Each drawing provides a link to a popup applet.

The faces of a convex hexahedron cannot have more than five sides; thus they are triangles, quadrilaterals or pentagons (no more than two).
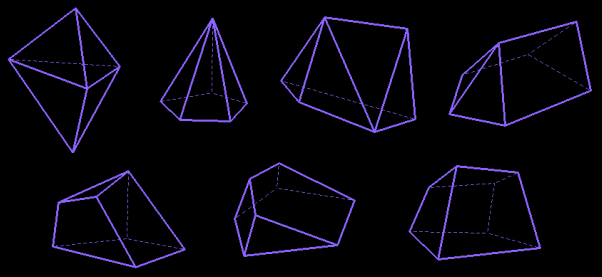
We know three classic types of hexahedra: the cobblestones (six quadrilaterals), the pyramids with pentagonal base and the diamonds (six triangles).
To discover the others we have to tire ourselves a little and to proceed with method:
•  list the possible combinations of faces,
•  eliminate those which are obviously impossible (one edge is the assembling of two sides of two faces, thus the total number s of sides must be even),
•  compute the numbers of edges (e=s/2) and of vertices (Euler formula v=e-4) for the others,
•  at last, draw the polyhedron... or prove that it don't exists... This is not always simple!

A less elementary method is to draw the seven Schlegel diagrams.

f3 f4 f5  e   v 
6
5
4
3
2
2
  		 
 
2
2
4
2
6 		 
1
 
1
 
2
  		9
10
10
11
11
12
12 		5
6
6
7
7
8
8
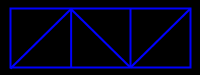
Here is the net of a representative of the first of these hexahedra. diamond
The cube is a representative of the last of these hexahedra; we can construct a representative of each of the six others from the cube using at most three cuttings. Try to draw them before to look at the answer.

The parallelepipeds are cobblestones whose opposite faces are parallel, therefore parallelograms. They fill the space.
The rectangular parallelepipeds have rectangular faces; the cube is a particular one (square faces).
The rhombohedra are parallelepipeds whose faces are identical rhombuses; we obtain them by distorting a cube along one of its diagonals.


parallelepiped


rectangular parallelepiped

rhombohedra (animations)

If we twist a rhombohedron around its axis, we get a family of curious equifacial cobblestones; without plane of symmetry, they exist in two mirror images forms (depending on the direction of the rotation). They are the duals of triangular antiprisms which have been stretched or compressed and then twisted (along and around their axis).

twisted rhombohedron (compressed cube) twisted cube twisted rhombohedron (stretched cube)

reference: hexahedra on Numericana

home page
French 		convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects April 1999
updated 11-03-2007