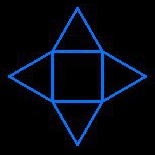
 square antiprism
square antiprism(assemble two pieces to create a ring of head to foot triangles)
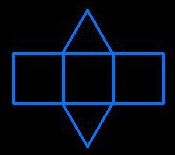 triangular prism
triangular prism 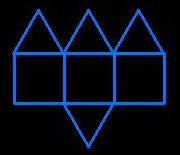 assembling
assemblingprism-tetrahedron
 assembling
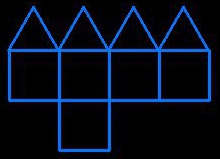
assemblingcube-pyramid
• assemblings of triangles and squares
8 triangles and 2 squares
 square antiprism
square antiprism(assemble two pieces to create a ring of head to foot triangles) |
2 triangles and 3 squares
 triangular prism
triangular prism |
4 triangles and 3 squares
 assembling
assemblingprism-tetrahedron |
4 triangles and 5 squares
 assembling
assemblingcube-pyramid |
• shadows of polyhedra
The following polyhedra may produce a square shadow :• cross sections of a cube
• To get a square we need to use a plane parallel to a face of the cube.|
• a nice equifacial polyhedron The polyhedron has 24 identical kite-shaped faces, each determined by one of the 3x8 cuts. Its edges and vertices belong to the planes and axes of symmetry of the cube.There are interesting cross-sections (into two symmetrical polyhedra): three parallel to the faces of the cube which are regular octagons, and four perpendicular to the diagonals of the cube which are regular hexagons. Its volume is one third of that of the cube (detailed proof). Net to download (A5 half net). |
|