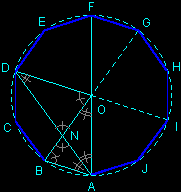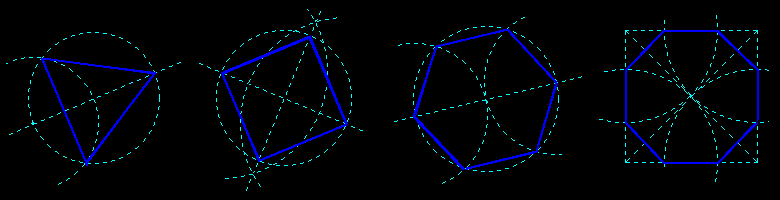
Remark: we can obviously construct a regular octagon starting from a circle with two perpendicular diameters and their bisectors;
the construction starting from a square proposed here, is less known (exercise: justify it!).
In a circle with two perpendicular diameters OA and OA', construct the circle with diameter OA'; its center is the midpoint M of OA'. The line AM intersects this little circle at P and Q. The circles with center A and going through P and Q cross the great circle on four vertices of the pentagon; the fifth vertex is diametrically opposite to A.
Remark: We can avoid the construction of the midpoint M using the perpendicular bisector of [OA'] by changing the drawing's order of the first two circles: start by drawing a straight line, choose a point M on it, and plot a circle of center M and diameter (OA '); then draw the circle of radius [OA']. The construction of a perpendicular bisector is however useful (but not necessary!) to obtain the diameter (OA) perpendicular to (OA ').
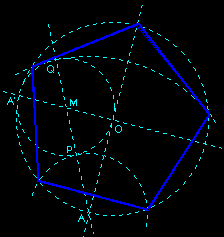
I find the proof of this construction nice; reasoning by analysis and synthesis deserves a pause.
Let us also take the opportunity to remind the theorems about the angle of a sector whose sides intersect a circle. To be concise, we will use the "classic" vocabulary (inscribed, central, inside, outside angle, when the vertex of the sector is on, at the center, inside, outside the circle), although it is incorrect to speak about the vertex or the sides of an angle. The angle is at the sector of what length is at the segment. Nobody would think of talking about the ends of a length!
• An inscribed angle is half the angle at the center that intercepts the same arc (the inscribed angle has same measure as the arc it intercepts).
• An outside angle is equal to the half-difference of the angles at the center intercepting the same arcs.
• An inside angle is equal to the half-sum of the angles at the center intercepting the same arcs.
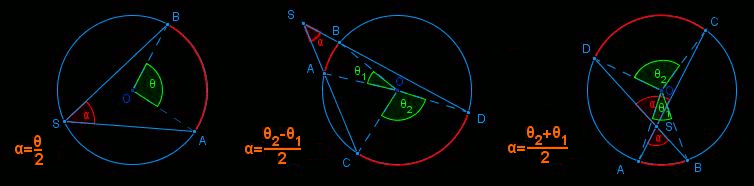
These results remain valid when one side of the sector (or both!) is tangent to the circle; a tangent is indeed the limit position of a secant.
With AB=x, AD=y and r radius of the circle, we have:
r=y-x because ABN and DON are isosceles in A and D (theorems above), so OD=ND=AD-AN=AD-AB,
r²=xy because AON and ADO are similar (they have the same angles), so AO/AD=AN/AO=AB/OA.
With y=r+x the second relation leads to the equation r²=x²+rx, which has only one positive solution.
• The construction proposed above provides precisely the only pair (x, y) satisfying these two properties: x=AP and y=AQ (radii of the two arcs of circles). Indeed in the right-angled triangle AMO we have AM²=OA²+OM² (Pythagoras' theorem), thus (x+r/2)²=r²+(r/2)², hence x²+rx=r²; we have also y=AP+PQ=x+r. And we are done!
Remarks: Knowing that φ²=1+1/φ where φ=(1+√5)/2 is the golden ratio, we compute x=r/φ and y=rφ.
OAB, ABN, DNO, ANO and OAD are all golden triangles.
The right-angled triangles ABF and ADF give (Pythagoras' theorem) the sides BF and DF of the regular star and convex pentagons, and we verify that the value of their ratio BF/DF is φ.
In a convex regular pentagon the ratio of the radius of the circumscribed circle to the side is about 0.85.