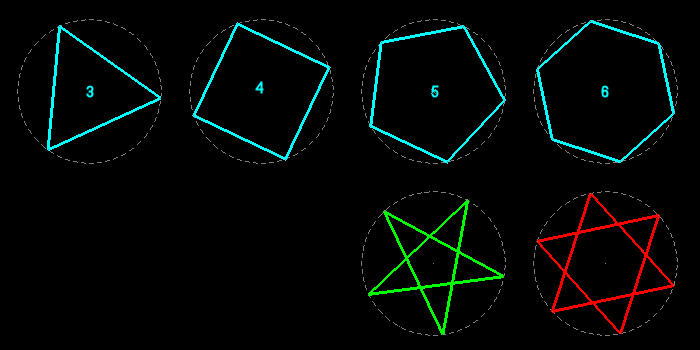
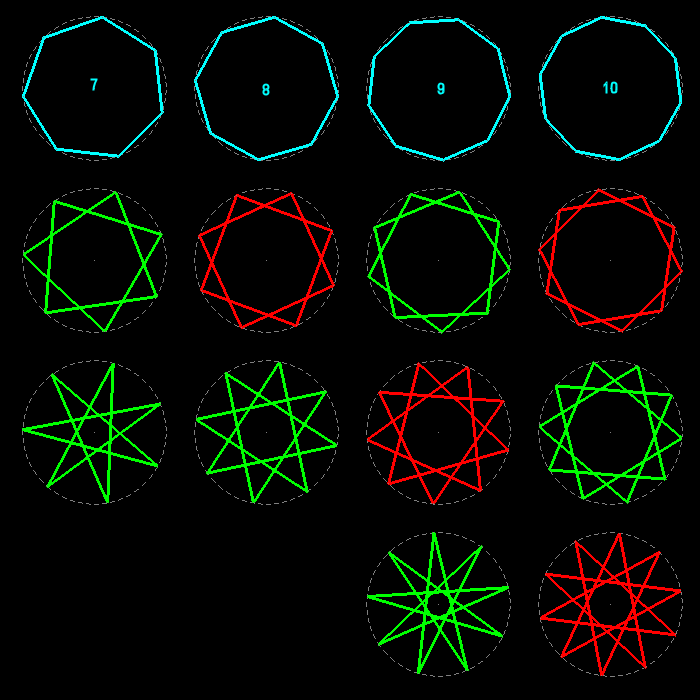
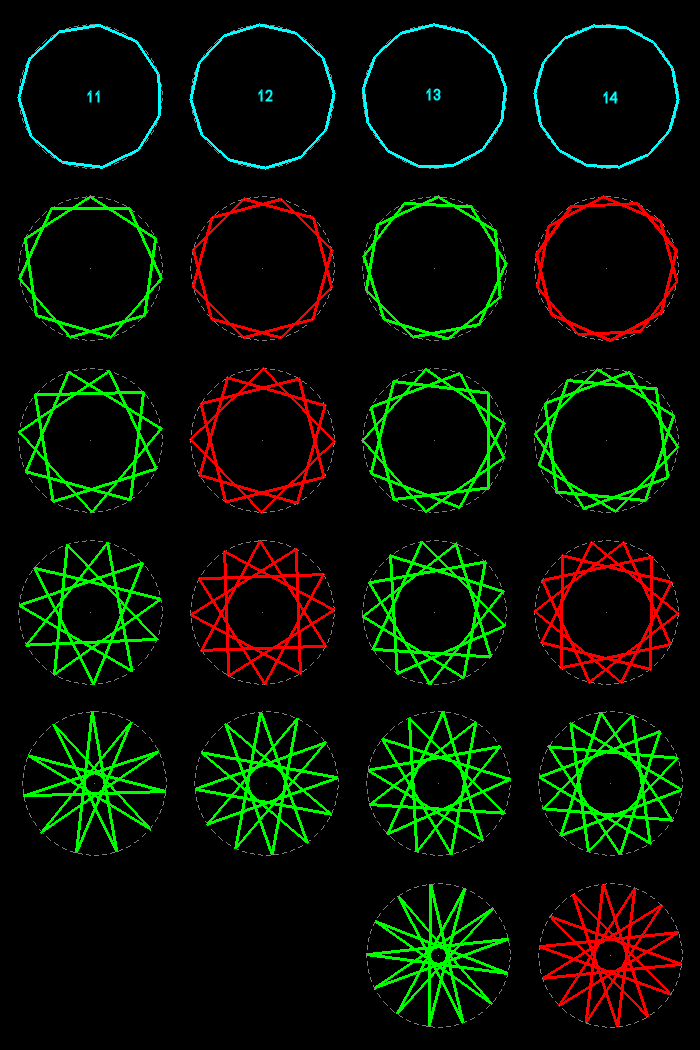
the regular polygons

The regular polygons are the analogues, in dimension two, of the regular polyhedra in dimension three and of the regular polytopes in dimension four. A regular polygon has all its sides equal and all its angles equal; its vertices are regularly distributed on a circle (their number n>2 is the order of the polygon).
The number of regular polygons is infinite, while there exists only a finite number of regular polyhedra or of regular polytopes. All these polygons are not constructible with ruler and compass.
We distinguish the convex polygons (all their diagonals are inside) and the star polygons (their sides are n diagonals of the convex ones). The star figures of order n are compounds of identical regular polygons of order k; they exist only for non prime orders greater than 5 and if k divides n.
The faces of the uniform polyhedra, therefore of the regular polyhedra and of the Archimedes' polyhedra, are regular polygons.

Here are all the regular polygons of orders 3 to 14; the star polygons and the star figures are shown under the convex polygons of same order.

polygons (3-4-5-6)
polygons (7-8-9-10)
polygons (11-12-13-14)


Remark: the areas of a square and a convex regular dodecagon inscribed in a circle of radius r are respectively 2r² and 3r².

A polygon (non necessarily regular) with n sides has n(n-3)/2 diagonals (if the polygon isn't convex, some are outside).
proof: from each of the n vertices we can draw n-1 segments (2 sides and n-3 diagonals), but then we have drawn them twice.
examples: 3(3-3)/2=0 thus a triangle has no diagonal, a quadrilateral has 4(4-3)/2=2 and a pentagon 5(5-3)/2=5 which are the sides of the stellated pentagon... a decagon has 35... a dodecagon 54... a 14-polygon 77...

home page
French 		convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects May 2000
updated 28-10-2004