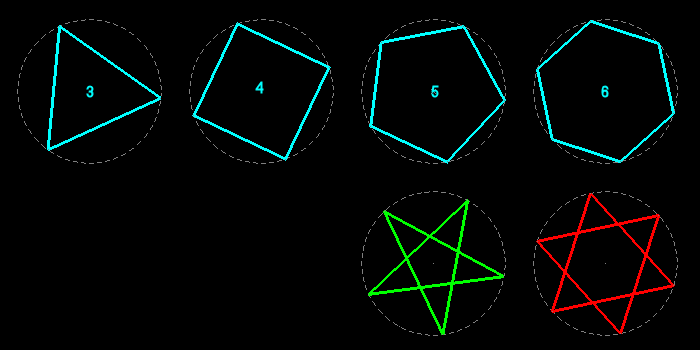
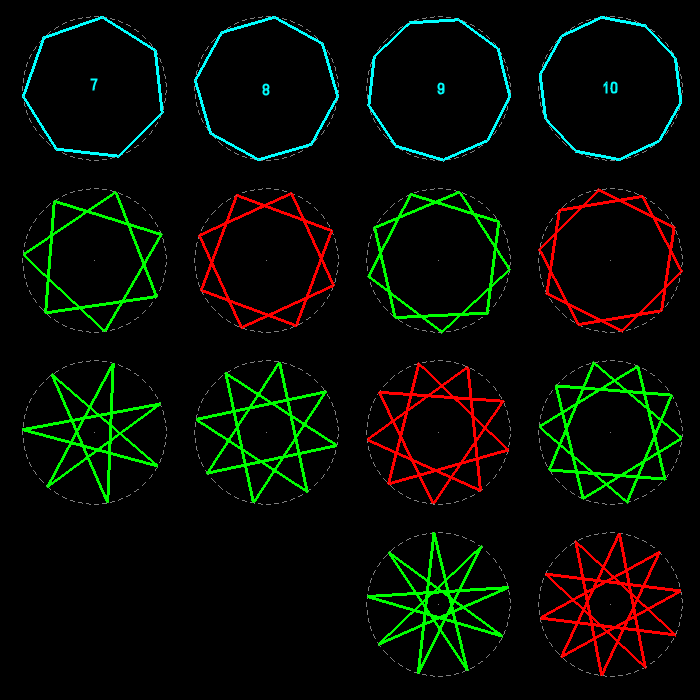
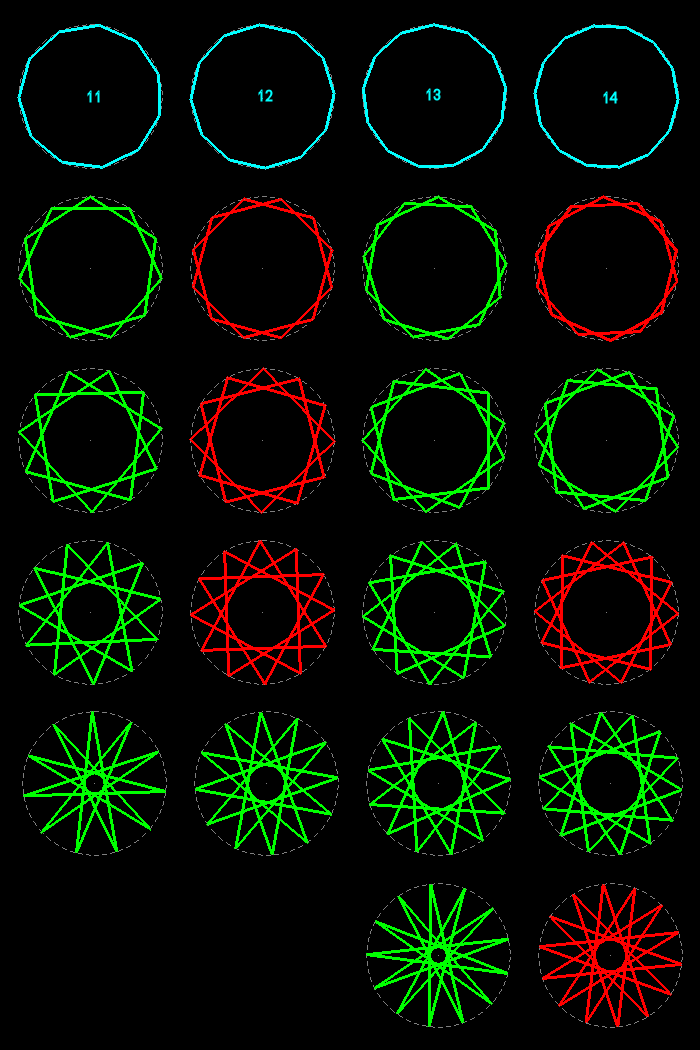
les polygones réguliers

Les polygones réguliers sont les analogues, en dimension deux, des polyèdres réguliers en dimension trois et des polytopes réguliers en dimension quatre. Un polygone régulier a tous ses côtés égaux et tous ses angles égaux ; ses sommets sont régulièrement répartis sur un cercle (leur nombre n>2 est l'ordre du polygone).
Le nombre des polygones réguliers est infini, alors qu'il n'existe qu'un nombre fini de polyèdres réguliers ou de polytopes réguliers. Tous ces polygones ne sont pas constructibles à la règle et au compas.
Ils peuvent être convexes (toutes leurs diagonales sont à l'intérieur) ou étoilés (leurs côtés sont n diagonales des convexes).
Les polygones réguliers composés d'ordre n, parfois appelés "étoiles", sont formés de polygones réguliers identiques d'ordre k ; ils n'existent que pour les ordres non premiers supérieurs à 5 et si k divise n.
Les faces des polyèdres uniformes, donc des polyèdres réguliers et des polyèdres archimédiens, sont des polygones réguliers.

Voici tous les polygones réguliers d'ordres 3 à 14 : les étoilés et les composés sont disposés sous les convexes de même ordre.

polygones (3-4-5-6)
polygones (7-8-9-10)
polygones (11-12-13-14)


Remarque : les aires d'un carré et d'un dodécagone régulier convexe inscrits dans un cercle de rayon r sont respectivement 2r² et 3r².

Un polygone (on nécessairement régulier) à n côtés a n(n-3)/2 diagonales (si le polygone n'est pas convexe, certaines sont à l'extérieur).
preuve : à partir de chacun des n sommets on peut tracer n-1 segments (2 côtés et n-3 diagonales), mais alors on les aura tracé deux fois.
exemples : 3(3-3)/2=0 donc un triangle n'a pas de diagonale, un quadrilatère en a 4(4-3)/2=2 et un pentagone 5(5-3)/2=5 qui sont les côtés du pentagone étoilé... un décagone en a 35... un dodécagone 54... un 14-polygone 77...

page accueil
anglais 		polyèdres convexes - polyèdres non convexes - polyèdres intéressants - sujets connexes mai 2000
mis à jour 28-10-2004