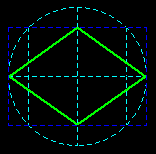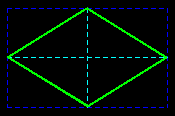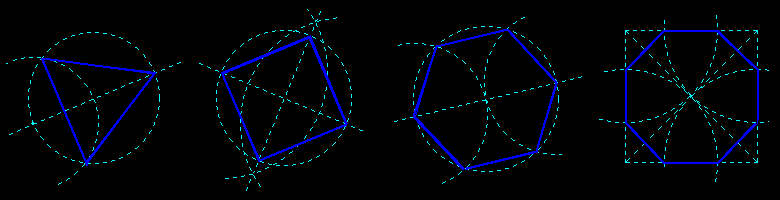
Remarque : on peut évidemment construire un octogone régulier à partir d'un cercle avec deux diamètres perpendiculaires et leurs bissectrices ;
la construction à partir d'un carré proposée ici est moins connue (exercice : la justifier !).
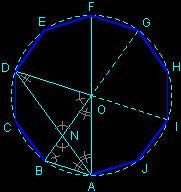
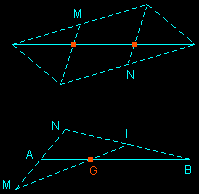
Dans un cercle muni de deux diamètres perpendiculaires (OA) et (OA'), on construit le cercle de diamètre [OA'] ; son centre est le milieu M de [OA']. La droite (AM) coupe ce petit cercle en P et Q. Les cercles de centre A passant par P et Q coupent le grand cercle en quatre sommets du pentagone ; le cinquième sommet est diamétralement opposé à A.
Remarque : On peut éviter la construction du milieu M à l'aide de la médiatrice de [OA'] en changeant l'ordre des tracés des deux premiers cercles : commencer par tracer une droite, y choisir un point M, et tracer un cercle de centre M et de diamètre (OA') ; puis tracer le cercle de rayon [OA']. La construction d'une médiatrice est cependant utile (mais pas nécessaire !) pour obtenir le diamètre (OA) perpendiculaire à (OA').
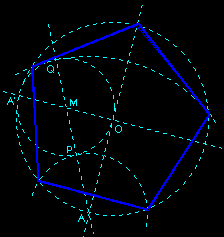
Je trouve la preuve de cette construction "jolie" ; le raisonnement par analyse et synthèse mérite qu'on s'y arrête un instant.
Profitons aussi de l'occasion pour rappeler les théorèmes sur l'angle d'un secteur dont les côtés sont sécants à un cercle. Pour être concis nous utiliseront le vocabulaire "classique" (angle inscrit, au centre, intérieur, extérieur quand le sommet du secteur se trouve sur, au centre, à l'intérieur, à l'extérieur du cercle) bien qu'il soit incorrect de parler du sommet ou des côtés d'un angle. L'angle est au secteur ce que la longueur est au segment. Personne ne songerait à parler des extrémités d'une longueur !
• Un angle inscrit est la moitié de l'angle au centre qui intercepte le même arc (l'angle inscrit a même mesure que l'arc qu'il intercepte).
• Un angle extérieur est égal à la demi-différence des angles au centre interceptant les mêmes arcs.
• Un angle intérieur est égal à la demi-somme des angles au centre interceptant les mêmes arcs.
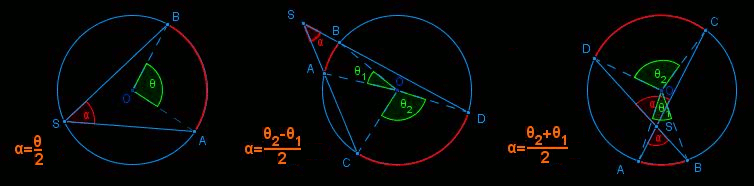
Ces résultats restent valables quant un côté du secteur (ou les deux !) est tangent au cercle ; une tangente est en effet la position limite d'une sécante.
Avec AB=x, AD=y et r rayon du cercle, on a :
r=y-x car ABN et DON sont isocèles en A et D (théorèmes ci-dessus), d'où OD=ND=AD-AN=AD-AB,
r²=xy car AON et ADO sont semblables (ils ont les mêmes angles), d'où AO/AD=AN/AO=AB/OA.
Avec y=x+r, la seconde relation conduit à l'équation r²=x²+rx, qui a seulement une solution positive.
• La construction proposée ci-dessus fournit justement l'unique couple (x,y) vérifiant ces deux propriétés : x=AP et y=AQ (rayons des deux arcs de cercles). En effet, dans le triangle rectangle AMO on a AM²=OA²+OM² (théorème de Pythagore), donc (x+r/2)²=r²+(r/2)², soit x²+rx=r² ; on a aussi y=AP+PQ=x+r. Et voilà !
remarques : Sachant que φ²=1+1/φ où φ=(1+√5)/2 désigne le nombre d'or, on calcule x=r/φ et y=rφ.
OAB, ABN, DNO, ANO et OAD sont tous des triangles d'or.
Les triangles rectangles ABF et ADF fournissent (théorème de Pythagore) les côtés BF et DF des pentagones étoilé et convexe, et on vérifie que BF/DF=φ.
Dans un pentagone régulier convexe le rapport du rayon du cercle circonscrit au côté est environ 0,85.