- construction classique -
- Michel Bataille -
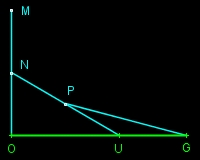
OM=UN=GP (N et P milieux de [OM] et [UN])
- Jo Niemeyer -

 |
 |
 |
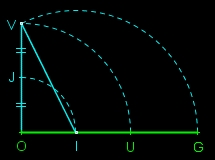
| à partir d'un triangle rectangle OIV avec OV=2×OI
- construction classique - |
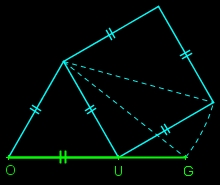
à partir d'un triangle équilatéral et d'un carré
- Michel Bataille - |
à partir de trois segments de même longueur
OM=UN=GP (N et P milieux de [OM] et [UN]) - Jo Niemeyer - |
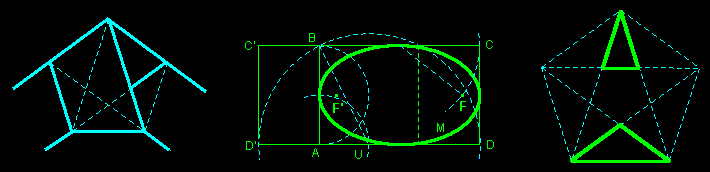 |
construction du pentagone régulier |
Une ellipse inscrite dans un rectangle d'or est une ellipse d'or (rapport des axes égal à φ).
Ses foyers F' et F sont faciles à construire (M étant un point de l'ellipse, si AB=1, alors MF'+MF = F'F² = φ). Son aire est πφ (pour AB=1).
Son excentricité e est égale à la distance foyer-directice d (si AB=2, alors e = d = 1/√φ).
Avec des suites de rectangles ou de triangles d'or emboîtés, on obtient facilement de jolies "spirales d'or". Ces tracés approchent des spirales logarithmiques, aussi appelées spirales équiangles (angle tangentiel constant) ou spirales de Bernoulli ; elles sont invariantes par similitude. Jacques Bernoulli a fait graver sur sa tombe "eadem mutata resurgo" que l'on peut traduire par "déplacée, je renais identique à moi-même".
Sur le dessin de gauche le centre de similitude est l'intersection des diagonales des rectangles, le rapport 1/φ, et l'angle -π/2 ; le rayon est donc multiplié par φ4≅6,9 à chaque tour. Sur la spirale de droite ce coefficient est environ 5, alors que pour la coquille du nautile (au milieu) il ne vaut qu'environ 3 !

Dame Nature utilise ces spirales pour assurer des croissances harmonieuses (fleurs, fruits, coquilles, cornes... galaxies).
| Des espèces végétales implantent des écailles (pomme de pin), des graines (tournesol)... sur une spirale en créant un objet tous les 137,5...°. Ces objets sont alors disposés en arcs de spirales orientées dans les deux sens ; les nombres d'arcs (dans les deux sens) sont deux nombres consécutifs de la suite de Fibonacci.
L'angle d'or ci-dessus correspond au partage du cercle en deux arcs de longueurs proportionnelles à 1 et φ : a/1 = b/φ = (a+b)/(1+φ) = 2π/φ² rad = 360°/φ². |
 |
| Rectangle d'or, ellipse d'or, pentagramme, spirale d'or... sont généralement considérés comme particulièrement harmonieux. Il n'est donc pas étonnant que le nombre d'or soit largement utilisé en peinture et en architecture.
Il apparaît par exemple dans la pyramide en verre du Louvre, à Paris : pour une base carrée de côté 2, sa hauteur est √φ (donc la hauteur principale de chacune de ses faces latérales est φ). Remarque : le triangle rectangle de côtés 1, √φ et φ (réciproque de Pythagore : 1+φ = φ²) conduit à un autre angle remarquable α = 51,827...° avec cos(α) = 1/φ et sin(α) = 1/√φ |
 |
| Avec une bande assez longue on peut réaliser cinq noeuds d'or régulièrement espacés. En recollant les extrémités on obtient ce bel anneau pentagonal qui est un ruban de Möbius : la bande n'a plus qu'une seule face et un seul bord ! |
 |
| Le pentagramme est le patron d'une pyramide remarquable dont les faces latérales sont des triangles d'or. Si le rayon de sa base est 1, alors sa hauteur est φ.
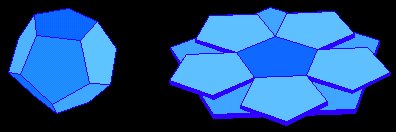
Si on assemble douze de ces pyramides sur les faces du dodécaèdre régulier, on obtient le petit dodécaèdre étoilé. |
animation |
|
Lors de la cérémonie de clôture des Jeux Olympiques 2000 de Sydney un dodécaèdre régulier a trôné au milieu du stade olympique ; l'idée de l'aplatir pour en faire une scène formée de deux demi-patrons était tout à fait originale et constituait un beau symbole : chaque face de ce polyèdre est un pentagone régulier dont le rapport de la diagonale au côté est égal au nombre d'or ! | |
 |
animation |
| références : |
• Fibonacci Numbers and the Golden Section (site)
• Le logo d'Alexander Bogomolny • Aux origines du nombre d'or (vidéo par El Jj) |
• Le nombre d'or par Thérèse Eveilleau
• Le nombre d'or : dossier par Robert Chalavoux • Le tournesol (dossier TPE) |
| Comme on l'a constaté, φ survient non seulement dans la réalité mathématique, parfois de façon inattendue, mais apparaît aussi dans la nature. L'esthétique de ce rapport est donc un bel exemple de "beauté mathématique".
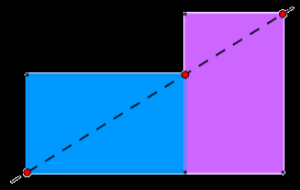
Cependant attention ! tout ce qui brille n'est pas d'or... En cherchant un peu, on peut trouver le nombre d'or dans de nombreux domaines : architecture, littérature, poésie, musique nature ... etc. exemple : Les cartes bancaires semblent être des rectangle d'or, mais leurs dimensions 54x86 mm sont seulement "proches" de deux nombres consécutifs de la suite de Fibonacci (55 et 89). Caractérisation géométrique : les deux rectangles identiques sont "d'or" si et seulement si les trois points rouges sont alignés. |
 | |
| trois bonnes références : | -> tout ce qui brille n'est pas d'or ! : la fin d'un mythe avec Géogébra... (en anglais)
Le nombre d'or Radiographie d'un mythe par Marguerite Neveux, suivi de La divine proportion par Herbert E. Huntley Le mythe du nombre d'or sur afis.org | |
page accueil
 |
polyèdres convexes - polyèdres non convexes - polyèdres intéressants - sujets connexes | août 1999 mis à jour 12-11-2024 |