- classical construction -
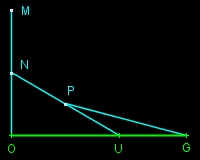
- Michel Bataille -
MO=NU=PG (N midpoint of [OM] and P of [UN])
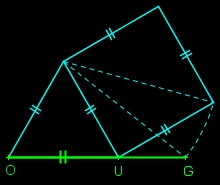
- Jo Niemeyer -

 |
 |
 |
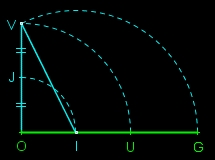
| starting from a rectangular triangle OIV with OV=2×OI
- classical construction - |
starting from an equilateral triangle and a square
- Michel Bataille - |
starting from three segments with same length
MO=NU=PG (N midpoint of [OM] and P of [UN]) - Jo Niemeyer - |
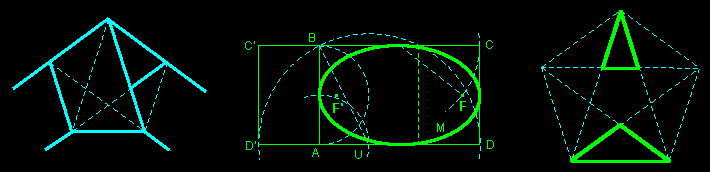 |
construction of the regular pentagon |
An ellipse inscribed in a golden rectangle is a golden ellipse (ratio of the axis equal to φ).
Its foci F' and F are easy to construct (M being a point on the ellipse, if AB=1 then MF'+MF = F'F² = φ). Its area is πφ (for AB=1).
Its eccentricity e is equal to the distance focus-directrix d (if AB=2 then e = d = 1/√φ).
With sequences of embedded golden rectangles or triangles, we get easily nice "golden spirals". These drawings are close to logarithmic spirals, also known as equiangle spirals (constant tangent angle) or Bernoulli's spirals; they are invariant by similitude. On Bernoulli's tombstone is engraved "eadem mutata resurgo" which can be translated by "moved, I rise again the same".
On the left drawing the center of similitude is the intersection of the rectangles' diagonals, the ratio 1/φ, and the angle -π/2; the radius is thus multiplied by φ4≅6,9 at each turn. On the spiral on the right this coefficient is around 5, while it is around 3 for the nautilus' shell!

Miss Nature uses them to provide harmonious growths (flowers, fruits, shells, horns... galaxies).
| Plant species implant scales (pine cone), seeds (sunflower)... on a spiral by creating an object every 137,5...°. These objects are then laid-out in arcs of spirals oriented in the two directions; the numbers of arcs (in the two directions) are two consecutive numbers of the Fibonacci's sequence.
The golden angle above corresponds to the division of the circle into two arcs with lengths proportional to 1 and φ: a/1 = b/φ = (a+b)/(1+φ) = 2π/φ² rad or 360°/φ². |
 |
| Golden rectangle, golden ellipse, pentagram, golden spiral... are generally considered as especially harmonious. It's not surprising that the golden ratio is widely used in painting and in architecture.
It appears for example in the glass pyramid of the Louvre, in Paris: for a square base with side 2, the altitude is √φ (thus the main altitude of each of its lateral face is φ). Remark: the rectangular triangle with sides 1, √φ and φ (converse of Pythagoras: 1+φ = φ²) leads to an other outstanding angle α = 51.827...° with cos(α) = 1/φ and sin(α) = 1/√φ |
 |
| With a strip long enough we may make five golden knots at regular intervals. By gluing the two ends together we get this nice pentagonal ring which is a Möbius strip: it has only one side and one "edge". |
 |
| The pentagram is the template of an outstanding pyramid whose lateral faces are golden triangles. If the radius of its base is 1 then its altitude is φ.
If we assemble twelve of such pyramids on the faces of the regular dodecahedron then we get the small stellated dodecahedron. |
animation |
|
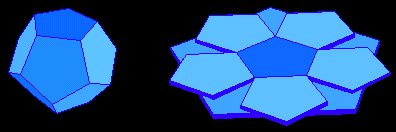
During the closing ceremony of the Sydney 2000 Olympic Games a regular dodecahedron sat enthroned in the center of the olympic stadium; the idea to flatten it in order to make a podium consisting of two half templates was quite original and constituted a nice symbol: each face of this polyhedron is a regular pentagon whose diagonal and side are in the golden ratio! | |
 |
animation |
| references: |
• Fibonacci Numbers and the Golden Section (site)
• Alexander Bogomolny's logo • Aux origines du nombre d'or (video by El Jj, in French) |
• Le nombre d'or by Thérèse Eveilleau (in French)
• Le nombre d'or by Robert Chalavoux (in French) • Le tournesol (student's work in French) |
| As we noticed, φ appears not only in the mathematical reality, sometimes in an unexpected way, but also in nature. The aesthetics of this ratio is therefore a fine example of "mathematical beauty".
However, be careful! all that glitters is not gold... If you look a little, you can find the golden ratio in many areas: architecture, literature, poetry, music, nature ... etc. example: The bank cards appear to be golden rectangles, but their dimensions 54x86 mm are only "close" to two consecutive numbers of the Fibonacci sequence (55 and 89). Geometric characterization: the two identical rectangles are "golden" if and only if the three red dots are aligned. |
 | |
| three good references: | -> all that glitters is not gold!: the end of a myth with Geogebra... | |
home page
 |
convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects | August 1999 updated 12-11-2024 |