the tilings of the plane

the seventeen groups of classical tilings

There are many examples of paving with figurative drawings in Maurits Cornelis Escher's work (end of the page).

the Penrose tilings

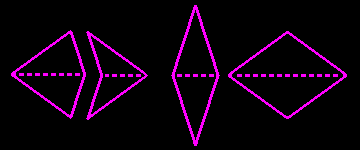
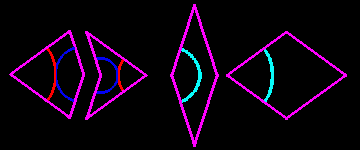
To get non-periodic tilings of the plane one must use a simple matching rule: tiles have to meet in a way such that each arc of each tile is connected with the arcs on the neighbored tiles. Since both sets use golden triangles, it makes sense that a kite and dart tiling can be translated into a rhombi tiling, and vice versa.
An other example of a tilling of this type designed by Nicolas Hannachi (one my notice an assembling condition).

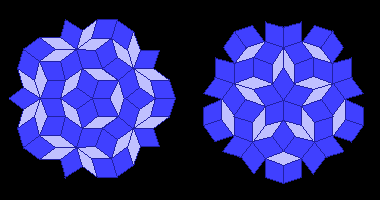
Discovered by Roger Penrose in 1974 these tilings have curious properties; among them:
  • any finite region of a Penrose tiling appears an infinity of times in any Penrose tiling,
  • there are small regions with a 5-fold symmetry,
  • if the tiling grows infinitely the ratio of the numbers of tiles in each type tends toward φ!
  • a rhombi tilling reveals a pattern of two types of overlapping decagons; the ratio of the two populations is φ!

an aperiodic tiling by John Conway (1937-2020)

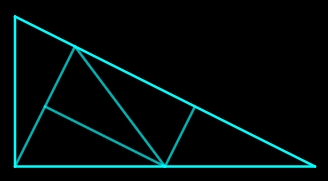
Divide a right-angle triangle of sides 1, 2 and √5 into five isometric triangles (and similar to the big triangle). Enlarge (factor 2) and divide each of these five triangles in the same way; iterate the process. We thus obtain a nice aperiodic tiling (no invariance by translation) whose triangles can take an infinity of different directions. Simplicity and beauty! Thank you John Conway.     reference: deux minutes pour Jonh Conway (youtube, in French)

aperiodic tilings with a single tile ("einstein" from German ein Stein, one stone)

    reference: "La quête du pavé apériodique unique"  by Jean-Paul Delahaye (in French)  Pour la Science n°433, November 2013

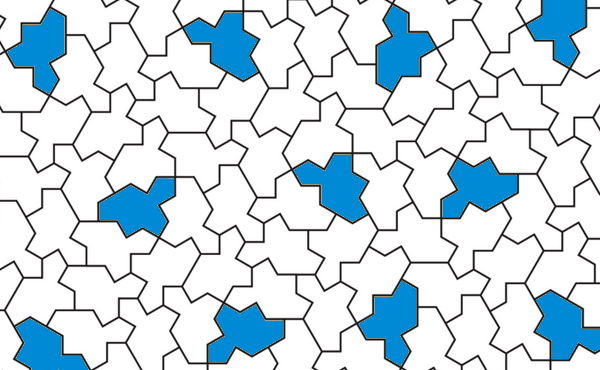
In the 1970s Roger Penrose showed that it was possible to tile the plane aperiodically by combining only two different tiles. But do aperiodic tilings with a single tile exist? Half a century later, in March 2023, a geometry enthusiast, David Smith, created an "einstein", a discovery confirmed by a team of four mathematicians: the "hat", a 13-sided polygon, assembly of eight kites arranged in a hexagonal network. One detail, however, bothered the purists: these aperiodic tilings used hats, some of which were turned over and which could therefore be considered as a second tile. A few weeks later the problem was solved with the creation of a pure "einstein" linked to the hat that its inventors named "spectre". This polygon has 14 sides of the same length and its angles measure 90°, 120° or 180° (starting from the vertex of the flat angle, we have alternately 120° and 90°). All tilings formed with this tile or its reflection are aperiodic, and no tiling composed of the spectre and its reflection is.     reference: A chiral aperiodic monotile (David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss)

tilings by Maurits Cornelis Escher

The Cairo tiling in two drawings by M.C. Escher (1967)

Fishes by M.C. Escher (1938, 1940 & 1943)
	Circle Limit III  (woodcut by M.C. Escher - 1959) This drawing also depicts a tiling, but here we are in the Poincaré disk, a model of the hyperbolic plane. Another world... • Hyperbolic tessellations  by David E. Joyce •  Hyperbolic planar tessellations  by Don Hatch

home page

convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects

February 2007 updated 01-06-2020