
only n rotations

n rotations and n reflections
| z → az+b | translation iff a=1, else rotation with center b/(1-a) and angle arg(a) |
| z → az+b | pure reflection iff ab+b=0 (axis with argument arg(a)/2 and going through the point b/2),
else glide reflection (axis with vector (ab+b)/2 and going through b/2) |
Below we'll focus on the groups G of isometries without translations (rosette) or whose translations built a normal sub-group TG generated over ℤ by one element (frieze) or two independent elements (wallpaper). The lattice is the orbit of the origin under TG (set of images of the origin by the translations); it is symmetric with respect to the origin.
For any isometry f of G we define the reduced isometry γ with the origin as fixed point by
if f(z)=az+b, then γ(z)=az, and else f(z)=az+b, then γ(z)=az.
These reduced isometries preserve the lattice and form the reduced group ΓG isomorph to the quotient group G/TG.
 |
rn = <r> = ΓR ≡ Cn
only n rotations |
 |
rnm = <r,m> = ΓR ≡ Dn
n rotations and n reflections |
| C1 | D1 | C2 | D2 | |||
| f11 ∞∞ F1 hop |
f1m ∞* F11 jump |
fm1 *∞∞ F12 sidle |
f1g ∞x F13 step |
f12 22∞ F2 spinning hop |
fmm *22∞ F21 spinning jump |
fmg 2*∞ F22 spinning sidle |
| no rotations | half turns | |||||
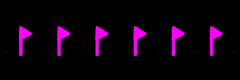 |
f11 = <t> ≡ C∞
ΓF = {id} ≡ C1 |
 |
f1m = <t,μ> ≡ C∞×D1
ΓF = {id,μ} ≡ D1 |
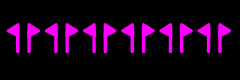 |
fm1 = <t,m>=<m',m"> ≡ D∞
ΓF = {id,m} ≡ D1 |
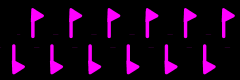 |
f1g = <g> ≡ C∞
ΓF = {id,μ} ≡ D1 |
 |
f12 = <t,r> = <r',r"> ≡ D∞
ΓF = {id,-id} ≡ C2 |
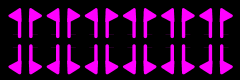 |
fmm = <t,r,μ> = <t,m,μ> ≡ D∞×D1
ΓF = {id,-id,m,μ} ≡ D2 |
 |
fmg = <m,r> = <r,g> = <m,g> ≡ D∞
ΓF = {id,-id,m,μ} ≡ D2 |
The group fmg is the one of the sinusoid.
The seven frameworks (symmetry axis and centers) of the friezes groups. | |
Above r, r' and r" denote central symmetries, m, m' and m" vertical mirror reflections, μ and g the mirror reflection and a glide reflection with axis Δ.
• Crystallographic notation: p or c for the lattice (primitive or centered) and 1,m,g,n as for the frieze groups (rotation rn f highest order).
• Orbifold notation(J.H. Conway): integer n for a set of rn rotations, * for a set of reflections, x for glide reflections (the half-turns after * have their centers on intersections of reflection axes).
• Notation of L. Fejes Tóth: Wnp
| C1 | D1 | C2 | D2 | C4 | D4 | C3 | D3 | C6 | D6 | |||||||
| p1 o W1 |
pm ** W12 |
pg xx W13 |
cm x* W11 |
p2 2222 W2 |
pmm *2222 W22 |
pmg 22* W23 |
pgg 22x W24 |
cmm 2*22 W21 |
p4 442 W4 |
p4m *442 W41 |
p4g 4*2 W42 |
p3 333 W3 |
p3m1 *333 W31 |
p31m 3*3 W32 |
p6 632 W6 |
p6m *632 W61 |
| no rotations | only half-turns | quarter turns | only thirds of turns | sixths of turns | ||||||||||||
| c1
c1- |
p
p- |
g
g- |
a
a- |
c2
c2+ |
p2
p2 |
pg
pg |
g2
g2+ |
a2
a2 |
c4
c4+ |
p2a2
p2a2 |
g2a2
g2a2 |
c3
c3+ |
a3
a3 |
a3c
a3+ |
c6
c6+ |
a6
a6 |
The key role played by the "fixed lines for W " associated to the axes of the reflections of the reduced group ΓW, and thus by the families of reflections in W, suggests a more simple and concise and more explicit notation (last two lines of the table above): p, g and a for each family of reflections (pure, glide, alternate), cn for the highest rotation's order n of the groups without reflections (if there are reflections n is the number of families, namely the sum of the exponents); we may add a sign - or + to specify that there are no rotations or rotations not centered on a reflection axis.
The name of each group ("pga" notation) is a link which opens a pop-up window with a tiling (table above) or a big sample of the pattern (drawings below).
On the graphics, in grey, the small polygons show the rotation's centers and orders, the full/dashed lines are the axes of the pure/glide reflections. In blue, a base of the lattice; in green, a generator set of the group.
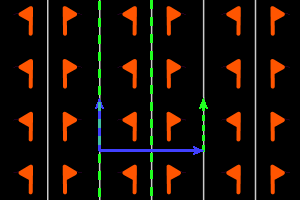
p- = <two pll m, one pll t> rectangular lattice, ΓW = D1 |
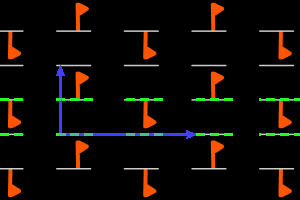
g- = <two pll g> rectangular lattice, ΓW = D1 |
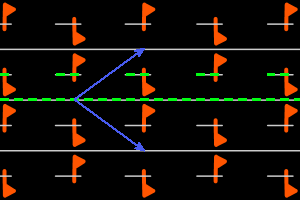
a- = <one m, one g pll> rhombic lattice, ΓW = D1 |
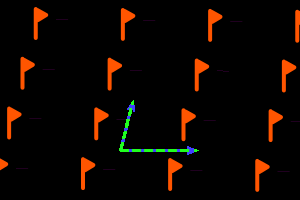
c1- =TW = <two t> oblique lattice, Γw = C1 |
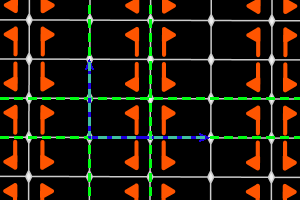
p2 = <four m (rectangle)> rectangular lattice, ΓW = D2 |
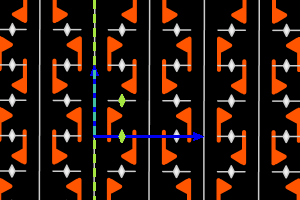
pg = <one m, two r2> rectangular lattice, ΓP = D2 |
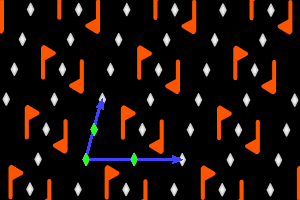
c2+ = <three r2> oblique lattice, ΓW = C2 |
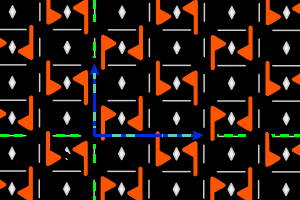
g2+ = <two ppd g> rectangular lattice, ΓW = D2 |
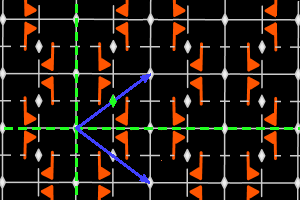
a2 = <two ppd m, one r2> rhombic lattice, ΓW = D2 |
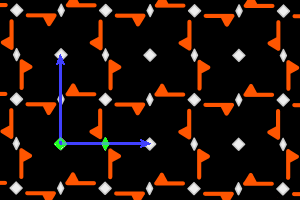
c4+ = <one r2, one r4> square lattice, ΓW = C4 |
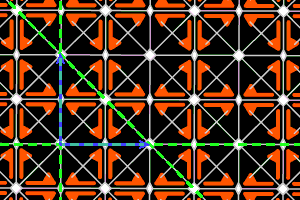
p2a2 = <three m (triangle 45,45,90)> square lattice, ΓW = D4 |
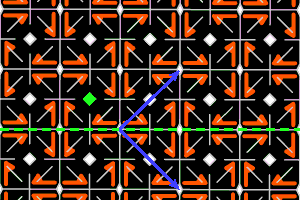
g2a2 = <one m, one r4> square lattice, ΓW = D4 |
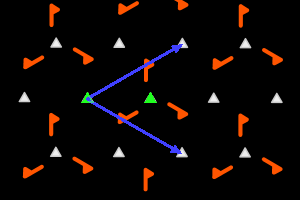
c3+ = <deux r3> hexagonal lattice, ΓW = C3 |
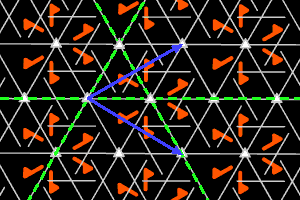
a3 = <three m (equilateral triangle)> hexagonal lattice, ΓW = D3 |
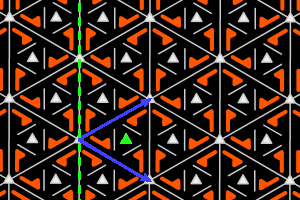
a3+ = <one m, one r3> hexagonal lattice, ΓW = D3 |
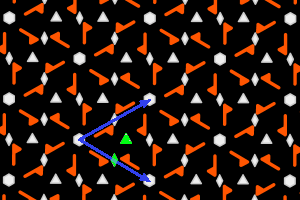
c6+ = <one r2, one r3> hexagonal lattice, ΓW = C6 |
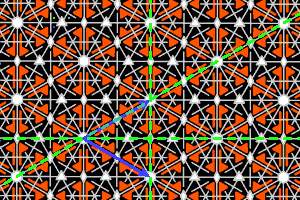
a6 = <three m (triangle 30,60,90)> hexagonal lattice, ΓW = D6 |
The 17 frameworks (reflection's axes and rotation's centers) of the tiling's groups. |
The method and the new results presented on this page are widely inspired from a research work by a dear friend, Georges Lion (1936-2014):
DISCRETE GROUPS OF PLANE ISOMETRIES - A new classification and their representations as Wallpaper groups. (Georges Lion, 2010)
Evgraf S. Fedorov described the 17 groups in 1891.
The Egyptian artists knew 12 of these types of pavings; the five missing groups are those which exhibit 3-fold symmetry.
Examples of 13 of these 17 types of paving appear on the mosaics of the Alhambra palace in Spain, near Granada (architecture of the Islamic Middle Ages where animal and human patterns where forbidden); the four missing groups are g-, c2+, g²+ and a³.
There are also many examples of paving with figurative drawings in Maurits Cornelis Escher's work.
Concerning the isohedral or tile-transitive tilings (for each pair of tiles there is an isometry in the group which sends one onto the other, the tiles are thus all identical), it's only in 1968 that H. Heesch described 28 types of tiles which pave the plane. This result, "forgotten" during about half a century, has been "cleaned" by John Conway and Xavier Hubaut (see last reference): the 28 types have been reduced to 19 because somes types are particular cases of others. For 15 of the 17 groups only one type of tile is associated to the group, and for each of the two groups with only glide reflections there are two.
You may view examples of tilings in the pop-up windows accessible from the table (a marked tile is necessary for a³).

these pictures come from here and here
a nice applet to explore the fifteen types
Wikipedia is also a good reference
| exercises: |
• Draw different pavings built with 2×1 rectangles, then establish the group of each paving (take the pleasure to search before referring to a few examples).
• There are 11 (semi)regular tilings with regular polygons: 3 regular with only one polygon, 6 with two polygons and 2 with three polygons. The corresponding groups are among the richest: some are obvious, can you find them all? • Which groups correspond to the 15 tilings with pentagons shown above? |
| video: | classer les pavages found on Youtube (in French): Deux minutes pour... (19' - 65 Mb) |
| algorithms: | tiling recognition by Brian Sanderson - reconnaissance des pavages by Nicolas Hannachi |
| references: |
• DISCRETE GROUPS OF PLANE ISOMETRIES - A new classification and their representations as Wallpaper groups.
by Georges Lion (2010) • The plane isometries, the frieze groups, the wallpaper groups ... on www.answers.com • A complete study of the plane isometries (450 Mb PDF, in French) • Conway's orbifold notation by J.H.Conway (English and Italian) • The Discontinuous Groups of Rotation and Translation in the Plane complete web pages by Xah Lee • Isometrica by George Baloglou • Subgroups lattices for crystallographic groups by Raymond F. Tennant • Tess is a program which allows you to achieve all types of symmetric drawings (used to generate the figures on this page) • with the applet Kali one can use all the above groups (downloadable program) • collections of patterns and tilings arranged by their symmetry groups, and much more! • Brian Sanderson's Pattern Recognition Algorithm - PDF version • Isohedrally compatible tilings by Philip M. Maynard • Tiling the plane with congruent pentagons by Doris Schattschneider • M.C. Escher: Vision of Symmetry by Doris Schattschneider, Abrams, New-york, 1990-2004 • Parcelles d'infini - Promenade au jardin d'Escher the figurative tilings of Alain Nicolas (in French) • the tessellation world of Makoto Nakamura deserves a visit • Groupes cristallographiques du plan (in French) by Xavier Hubaut (an other approach with the rotation's centers) - copy of the pdf version • Les pavages du plan (in French) by Xavier Hubaut: examples with drawings by M.C. Escher - copy of the pdf version • Eschersket is a drawing tool by Anselm Levskaya for exploring symmetrical patterns and designs which can export pictures and pattern tiles |
home page
 |
convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects | February 2007 updated 18-06-2023 |