
seulement n rotations

n rotations et n réflexions
| z → az+b | translation ssi a=1, sinon rotation de centre d'affixe b/(1-a) et d'angle arg(a) |
| z → az+b | réflexion pure ssi ab+b=0 (axe d'angle arg(a)/2 et passant par le point d'affixe b/2),
sinon réflexion glissée (axe de vecteur d'affixe (ab+b)/2 et passant par le point d'affixe b/2) |
Ci-dessous on s'intéresse aux groupes G d'isométries sans translation (rosace) ou dont les translations forment un sous-groupe normal TG engendré sur ℤ par un élément (frise) ou deux éléments indépendants (pavage). Le réseau est l'orbite de l'origine sous l'action de TG (ensemble des images de l'origine par les translations) ; il est symétrique par rapport à l'origine.
Pour toute isométrie f de G on définit l'isométrie réduite γ admettant l'origine comme point fixe par
si f(z)=az+b, alors γ(z)=az, et si f(z)=az+b, alors γ(z)=az.
Ces isométries réduites préservent le réseau et forment le groupe réduit ΓG isomorphe au groupe quotient G/TG .
 |
rn = <r> = ΓR ≡ Cn
seulement n rotations |
 |
rnm = <r,m> = ΓR ≡ Dn
n rotations et n réflexions |
| C1 | D1 | C2 | D2 | |||
| f11 ∞∞ F1 hop |
f1m ∞* F11 jump |
fm1 *∞∞ F12 sidle |
f1g ∞x F13 step |
f12 22∞ F2 spinning hop |
fmm *22∞ F21 spinning jump |
fmg 2*∞ F22 spinning sidle |
| pas de rotations | demi-tours | |||||
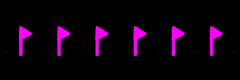 |
f11 = <t> ≡ C∞
ΓF = {id} ≡ C1 |
 |
f1m = <t,μ> ≡ C∞×D1
ΓF = {id,μ} ≡ D1 |
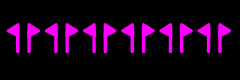 |
fm1 = <t,m>=<m',m"> ≡ D∞
ΓF = {id,m} ≡ D1 |
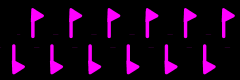 |
f1g = <g> ≡ C∞
ΓF = {id,μ} ≡ D1 |
 |
f12 = <t,r> = <r',r"> ≡ D∞
ΓF = {id,-id} ≡ C2 |
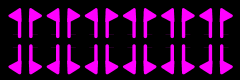 |
fmm = <t,r,μ> = <t,m,μ> ≡ D∞×D1
ΓF = {id,-id,m,μ} ≡ D2 |
 |
fmg = <m,r> = <r,g> = <m,g> ≡ D∞
ΓF = {id,-id,m,μ} ≡ D2 |
Le groupe fmg est celui de la sinusoïde.
Les sept canevas (axes et centres de symétrie) de ces groupes. | |
Ci-dessus r, r' et r" désignent des symétries centrales, m, m' et m" des réflexions d'axes verticaux, μ et g la réflexion et un glissage d'axe Δ.
• Notation cristallographique : p ou c pour le réseau (primitif ou centré) et 1,m,g,n comme pour les groupes de frises (rotations rn d'ordre maximum).
• Notation "orbifold" (J.H. Conway) : entier n pour un ensemble de rotations rn, * pour un ensemble de réflexions, x pour des réflexions glissées (les rotations après * ont leurs centres à des intersections d'axes de réflexions).
• Notation de L. Fejes Tóth : Wnp
| C1 | D1 | C2 | D2 | C4 | D4 | C3 | D3 | C6 | D6 | |||||||
| p1 o W1 |
pm ** W12 |
pg xx W13 |
cm x* W11 |
p2 2222 W2 |
pmm *2222 W22 |
pmg 22* W23 |
pgg 22x W24 |
cmm 2*22 W21 |
p4 442 W4 |
p4m *442 W41 |
p4g 4*2 W42 |
p3 333 W3 |
p3m1 *333 W31 |
p31m 3*3 W32 |
p6 632 W6 |
p6m *632 W61 |
| pas de rotations | demi-tours seulement | quarts de tours | tiers de tours seulement | sixièmes de tours | ||||||||||||
| c1
c1- |
p
p- |
g
g- |
a
a- |
c2
c2+ |
p2
p2 |
pg
pg |
g2
g2+ |
a2
a2 |
c4
c4+ |
p2a2
p2a2 |
g2a2
g2a2 |
c3
c3+ |
a3
a3 |
a3c
a3+ |
c6
c6+ |
a6
a6 |
Le rôle clef joué par les "droites fixes pour P " associées aux axes des réflexions du groupe réduit ΓP, et donc par les familles de réflexions de P, suggère une notation plus simple et concise et plus explicite (deux dernières lignes du tableau ci-dessus) : p, g et a pour chaque famille de réflexions (pures, glissées, alternées), cn pour l'ordre maxi n des rotations des groupes sans réflexions (s'il y a des réflexions cet ordre est le nombre de familles, soit la somme des exposants) ; on pourrait ajouter un signe - ou + pour préciser qu'il n'y pas de rotations ou des rotations non centrées sur un axe de réflexion.
Le nom de chaque groupe (notation "pga") est un lien qui ouvre une fenêtre pop-up avec un pavage (tableau ci-dessus) ou un grand échantillon du motif (dessins ci-dessous).
Sur les dessins, en gris, les petits polygones indiquent les centres et ordres des rotations, et les droites pleines/pointillées sont les axes des réflexions pures/glissées. En bleu, une base du réseau ; en vert, un système générateur du groupe.
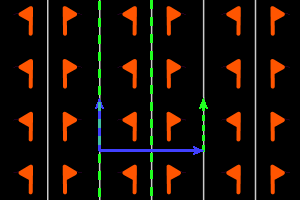
p- = <deux m pll, une t pll> réseau rectangulaire, ΓP = D1 |
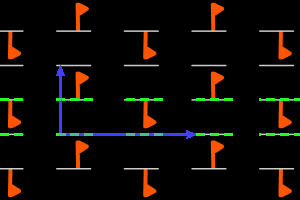
g- = <deux g pll> réseau rectangulaire, ΓP = D1 |
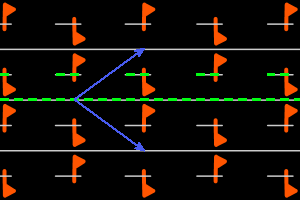
a- = <une m, une g pll> réseau rhombique, ΓP = D1 |
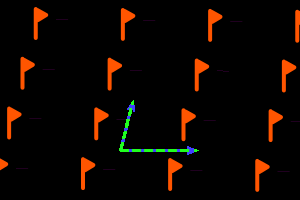
c1- =TP = <deux t> réseau oblique, ΓP = C1 |
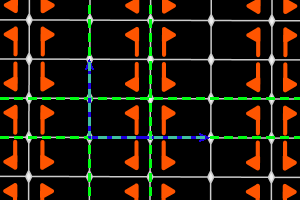
p2 = <quatre m (rectangle)> réseau rectangulaire, ΓP = D2 |
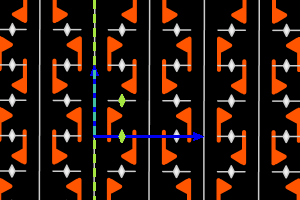
pg = <une m, deux r2> réseau rectangulaire, ΓP = D2 |
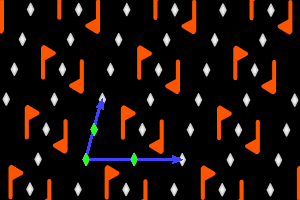
c2+ = <trois r2> réseau oblique, ΓP = C2 |
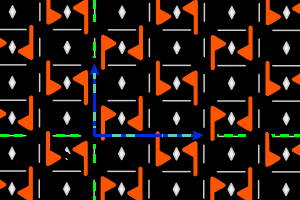
g2+ = <deux g ppd> réseau rectangulaire, ΓP = D2 |
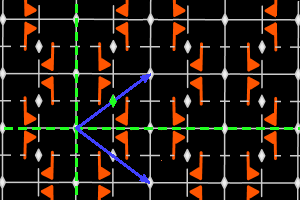
a2 = <deux m ppd, une r2> réseau rhombique, ΓP = D2 |
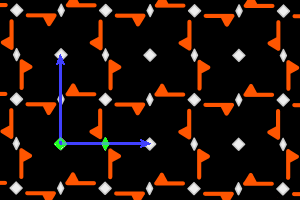
c4+ = <une r2, une r4> réseau carré, ΓP = C4 |
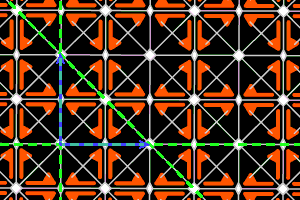
p2a2 = <trois m (triangle 45,45,90)> réseau carré, ΓP = D4 |
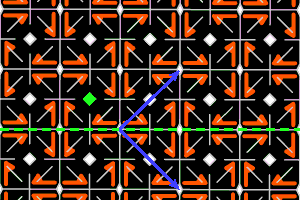
g2a2 = <une m, une r4> réseau carré, ΓP = D4 |
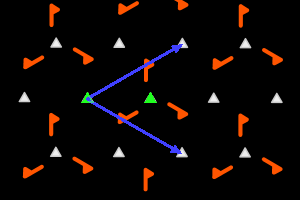
c3+ = <deux r3> réseau hexagonal, ΓP = C3 |
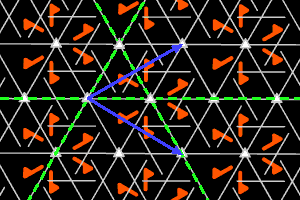
a3 = <trois m (triangle équilatéral)> réseau hexagonal, ΓP = D3 |
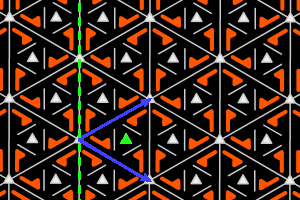
a3+ = <une m, une r3> réseau hexagonal, ΓP = D3 |
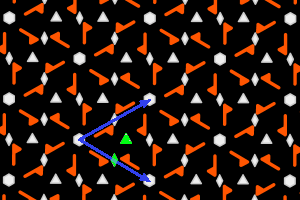
c6+ = <une r2, une r3> réseau hexagonal, ΓP = C6 |
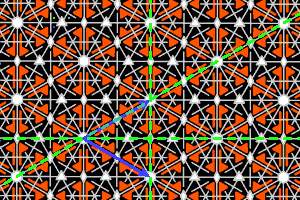
a6 = <trois m (triangle 30,60,90)> réseau hexagonal, ΓP = D6 |
Les 17 canevas (axes des réflexions et centres des rotations) des groupes de pavages. |
La méthode et les nouveaux résultats exposés sur cette page sont largement inspirés par un travail de recherche d'un ami cher, Georges Lion (1936-2014) :
DISCRETE GROUPS OF PLANE ISOMETRIES - A new classification and their representations as Wallpaper groups. (Georges Lion, 2010)
Evgraf S. Fedorov a décrit les 17 groupes en 1891.
Les artistes égyptiens connaissaient 12 de ces types de pavages ; les cinq groupes absents sont ceux avec des symétries d'ordre 3.
Des exemples de 13 de ces 17 types de pavage apparaissent sur les mosaïques du palais de l'Alhambra près de Grenade en Espagne (architecture du Moyen Âge islamique où les motifs animaliers ou humains étaient interdits) ; les quatre groupes absents sont g-, c2+, g²+ et a³.
On trouve aussi de nombreux exemples de pavages avec des dessins figuratifs dans l'œuvre de Maurits Cornelis Escher.
Concernant les pavages isoédriques ou pavé-transitifs (pour toute paire de pavés il existe une isométrie du groupe qui transforme l'un en l'autre, les pavés sont donc tous identiques), ce n'est qu'en 1968 que H. Heesch a caractérisé 28 types de pavés asymétriques qui pavent le plan. Ce résultat, "oublié" pendant près d'un demi-siècle, a été "nettoyé" par John Conway et Xavier Hubaut (voir dernière référence) : les 28 types ont été réduits à 19, car certains types sont des cas particuliers d'autres. Pour 15 des 17 groupes un seul type de pavé est associé au groupe, et pour chacun des deux groupes ne contenant que des réflexions glissées il y en a deux.
Vous pouvez voir des exemples de pavages dans les fenêtres pop-up accessibles depuis la table (un pavé marqué est nécessaire pour a³).

ces images viennent de là et là
une belle animation pour explorer les quinze types
Wikipedia est aussi une bonne référence (en anglais)
| exercices : |
• Dessiner différents pavages constitués de rectangles 2×1, puis déterminer le groupe de chaque pavage (prendre le plaisir de chercher avant de consulter quelques exemples).
• Il y a 11 pavages (semi)réguliers avec des polygones réguliers : 3 réguliers avec seulement un polygone, 6 avec deux polygones et 2 avec trois polygones. Les groupes correspondants sont parmi les plus riches : certains sont évidents, pouvez-vous les trouver tous ? • Quels groupes correspondent aux 15 pavages avec des pentagones représentés ci-dessus ? |
| vidéo : | classer les pavages trouvée sur Youtube : Deux minutes pour... (19' - 65 Mo) |
| algorithmes : | tiling recognition par Brian Sanderson (en anglais) - reconnaissance des pavages par Nicolas Hannachi |
| références : |
• DISCRETE GROUPS OF PLANE ISOMETRIES - A new classification and their representations as Wallpaper groups.
par Georges Lion (2010, en anglais) • Les isométries planes, les groupes de frises, les groupes de pavages ... sur www.answers.com (en anglais) • Une étude complète des isométries planes (PDF de 450 Ko, en français) • La notation "orbifold" de J.H.Conway (en anglais et italien) • The Discontinuous Groups of Rotation and Translation in the Plane pages web très complètes de Xah Lee (en anglais) • Isometrica par George Baloglou (en anglais) • Subgroups lattices for crystallographic groups par Raymond F. Tennant (en anglais) • Tess est un programme de dessins symétriques (utilisé pour les figures de cette page) • avec l'applet Kali on peut utiliser tous les groupes ci-dessus (programme téléchargeable) • collections de motifs et de pavages organisées selon leurs groupes de symétrie, et bien davantage ! (en anglais) • Pattern Recognition Algorithm de Brian Sanderson (un algorithme pour reconnaître le groupe d'un pavage, en anglais) et exemples de pavages • Isohedrally compatible tilings par Philip M. Maynard (en anglais) • Tiling the plane with congruent pentagons par Doris Schattschneider (en anglais) • M.C. Escher: Vision of Symmetry par Doris Schattschneider, Abrams, New-york, 1990-2004 (en anglais) • Parcelles d'infini - Promenade au jardin d'Escher les pavages figuratifs de Alain Nicolas • le monde des pavages de Makoto Nakamura mérite une visite • Groupes cristallographiques du plan de Xavier Hubaut (une autre approche par les centres de rotations) - copie de la version pdf • Les pavages du plan de Xavier Hubaut : exemples avec des dessins de M.C. Escher - copie de la version pdf • Eschersket est un outil de dessin d'Anselm Levskaya permettant d'explorer des motifs symétriques ; il peut exporter des images et des pavés (en anglais) |
page accueil
 |
polyèdres convexes - polyèdres non convexes - polyèdres intéressants - sujets connexes | février 2007 mis à jour 18-06-2023 |