
On trouve de nombreux exemples de pavages avec des dessins figuratifs dans l'œuvre de Maurits Cornelis Escher (fin de page).
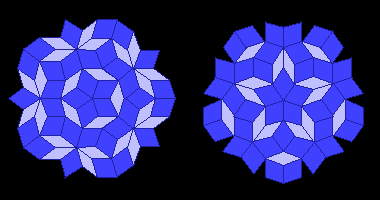
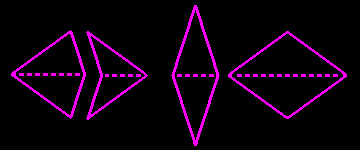
En assemblant deux triangles d'or identiques on obtient deux paires de quadrilatères (flèche et cerf-volant - losanges maigres et gras) qui permettent de réaliser de beaux pavages avec une symétrie d'ordre 5 (étoiles et soleils ci-dessous).
 |
 |
 |
 |
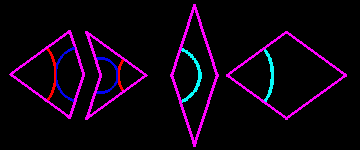
Pour obtenir des pavages non périodiques du plan on doit utiliser une règle d'assemblage : les pavés doivent être disposés de manière à ce que chaque arc de chaque pavé soit connecté aux arcs des pavés voisins. Comme les deux paires utilisent des triangles d'or, on comprend qu'un pavage de flèches et cerfs-volants peut être traduit en un pavage de losanges, et vice versa.
Un autre exemple d'un pavage de ce type imaginé par Nicolas Hannachi (on peut y remarquer une condition d'assemblage).
 |
 |
Découverts par Roger Penrose en 1974, ces pavages ont de curieuses propriétés, parmi lesquelles :
• toute région finie d'un pavage de Penrose apparaît une infinité de fois dans tout pavage de Penrose,
• il existe de petites régions avec une symétrie d'ordre 5,
• quand le pavage tend vers l'infini le rapport des nombres de pavés des deux types tend vers φ !
• un pavage de losanges révèle un motif de deux types de décagones qui se chevauchent ; le rapport de leurs populations est φ !
| références : |
• Penrose tilings par Eric Hwang - Penrose tilings of the plane par Ianiv Schweber (en anglais)
• Penrose tiling applet ( télécharger penrose.jar puis l'ouvrir avec Java) • un générateur de pavages de Penrose par J.-L. Sigrist |
 | |
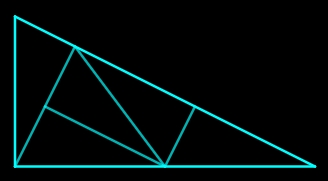
| Partagez un triangle rectangle de côtés 1, 2 et √5 en cinq triangles isométriques (et semblables au grand triangle). Agrandissez (facteur 2) et partagez chacun des cinq triangles de la même manière ; itérez le processus.
On obtient ainsi un joli pavage apériodique (pas d'invariance par translation) dont les triangles peuvent prendre une infinité de directions différentes Simplicité et beauté ! Merci John Conway. référence : deux minutes pour Jonh Conway (youtube) |
 |
référence : "La quête du pavé apériodique unique" par Jean-Paul Delahaye (Pour la Science n°433, novembre 2013)
| Dans les années 1970 Roger Penrose a montré qu’il était possible de paver le plan de façon apériodique en combinant seulement deux tuiles différentes. Mais existe-t-il des pavages apériodiques avec une seule tuile ?
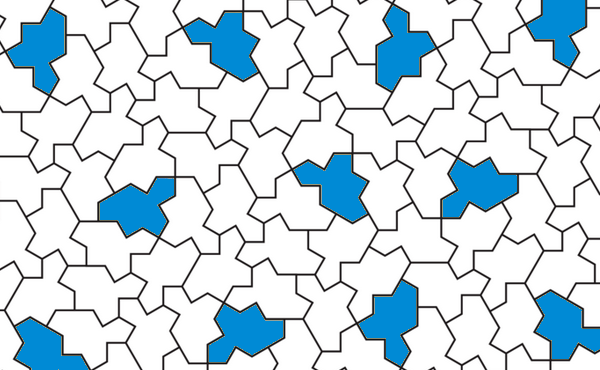
Un demi-siècle plus tard, en mars 2023, un amateur de géométrie, David Smith, a créé un "einstein", découverte confirmée par une équipe de quatre mathématiciens : le "chapeau", un polygone à 13 côtés, assemblage de huit cerf-volants disposés dans un réseau hexagonal. Un détail chagrinait cependant les puristes : ces pavages apériodiques utilisaient des chapeaux dont certains étaient retournés et que l'on pouvait donc considérer comme une seconde tuile. Quelques semaines plus tard le problème était résolu avec la création d'un pur "einstein" lié au chapeau que ses inventeurs nommèrent "spectre". Ce polygone a 14 côtés de même longueur et ses angles mesurent 90°, 120° ou 180° (en partant du sommet de l'angle plat on a alternativement 120° et 90°).
|

 |
 |
 |
 |
 |
 |
 |
| Le pavage du Caire dans deux dessins de M.C. Escher (1967) | |||
 |
 |
 |
| Poissons de M.C. Escher (1938, 1940 & 1943) | ||
 |
Circle Limit III (sculpture sur bois de M.C. Escher - 1959) Ce dessin représente aussi un pavage, mais nous sommes ici dans le disque de Poincaré, un modèle du plan hyperbolique. Un autre monde... • Hyperbolic tessellations par David E. Joyce
| |
page accueil
 |
polyèdres convexes - polyèdres non convexes - polyèdres intéressants - sujets connexes | février 2007 mis à jour 18-06-2023 |