
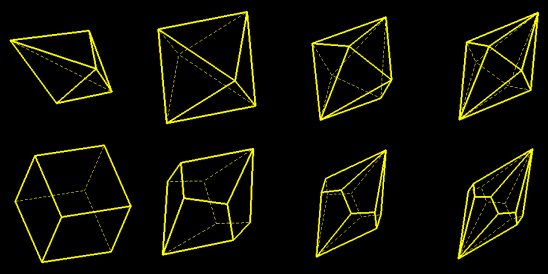
Ces polyèdres semi-réguliers convexes sont les duals des polyèdres archimédiens. Leurs faces sont superposables (mais pas régulières) et tangentes à une sphère (sphère inscrite) ; leurs sommets sont réguliers (de deux ou trois ordres).

Chaque dessin propose un lien vers un pop-up applet (davantage sur les caractéristiques des polyèdres semi-réguliers).
|
|
Le dual du cuboctaèdre (resp. de l'icosidodécaèdre) a 12 (resp. 30) faces en losanges.
Ses sommets d'ordre 3 sont les sommets d'un cube (resp. d'un dodécaèdre régulier) ; les sommets restants sont ceux d'un octaèdre (resp. d'un icosaèdre) régulier. On peut donc les réaliser ces polyèdres en assemblant des pyramides régulières à base carrée (resp. pentagonale) sur chaque face d'un cube (resp. d'un dodécaèdre régulier), ou des tétraèdres sur les faces d'un octaèdre (resp. icosaèdre) régulier.
|
| ||||||
|
|
Les duals du snub cube et du snub dodécaèdre ont respectivement 24 et 60 faces pentagonales.
|
| ||||||
Ces duals des prismes et des antiprismes complètent la liste des polyèdres semi-réguliers de seconde espèce.
(Le diamant d'ordre 4 est l'octaèdre régulier ; l'antidiamant d'ordre 3 est le cube.)
page accueil
 |
polyèdres convexes - polyèdres non convexes - polyèdres intéressants - sujets connexes | mars 1999 mis à jour 21-09-2004 |