
These semi-regular polyhedra of the second kind are the duals of the Archimedes' polyhedra. Their faces are superimposable (but not regular) and tangent to a sphere (inscribed sphere); their vertices are regular (of two or three types).

Each drawing provides a link to a popup applet (more about the characteristics of the semi-regular polyhedra).
|
|
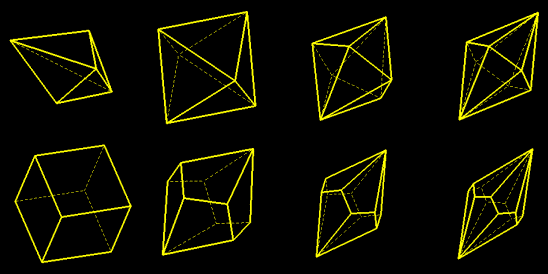
The dual of the cuboctahedron (resp. icosidodecahedron) has 12 (resp. 30) rhombic faces.
Its vertices of order 3 are the vertices of a cube (resp. a regular dodecahedron); the remaining vertices are those of a regular octahedron (resp. icosahedron). Thus these polyhedra can be made by assembling regular pyramids with a square (resp. pentagonal) base on each face of a cube (resp. a regular dodecahedron), or by assembling tetrahedra on the faces of a regular octahedron (resp. icosahedron).
|
| ||||||
|
|
The duals of the snub cube and of the snub dodecahedron have respectively 24 and 60 pentagonal faces.
|
| ||||||
These duals of the prisms and of the antiprisms complete the list of the second kind semiregular polyhedra.
(The diamond of order 4 is the regular octahedron; the antidiamond of order 3 is the cube.)
home page
 |
convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects | March 1999 updated 21-09-2004 |