


Le jeu de construction Geomag est une autre façon d'explorer le monde des polyèdres ; voici un bel exemple.
Voici les caractéristiques des polyèdres semi-réguliers de première espèce (pour leurs duals il suffit d'échanger s et f) :
| s | a | f | f3 | f4 | f5 | f6 | f8 | f10 | fn | polyèdre dual (face) | ||
| tétraèdre tronqué | 12 | 18 | 8 | 4 | - | - | 4 | - | - | - | triakis-tétraèdre (triangle isocèle) | |
| cube tronqué | 24 | 36 | 14 | 8 | - | - | - | 6 | - | - | triakis-octaèdre (triangle isocèle) | |
| octaèdre tronqué | 24 | 36 | 14 | - | 6 | - | 8 | - | - | - | tétrakis-hexaèdre (triangle isocèle) | |
| cuboctaèdre | 12 | 24 | 14 | 8 | 6 | - | - | - | - | - | dodécaèdre rhombique (losange) | |
| petit rhombicuboctaèdre | 24 | 48 | 26 | 8 | 18 | - | - | - | - | - | icositétraèdre deltoïdal (cerf-volant) | |
| grand rhombicuboctaèdre | 48 | 72 | 26 | - | 12 | - | 8 | 6 | - | - | disdyakis-dodécaèdre (triangle) | |
| snub cube | 24 | 60 | 38 | 32 | 6 | - | - | - | - | - | icositétraèdre pentagonal (pentagone) | |
| dodécaèdre tronqué | 60 | 90 | 32 | 20 | - | - | - | - | 12 | - | triakis-dodécaèdre (triangle isocèle) | |
| icosaèdre tronqué | 60 | 90 | 32 | - | - | 12 | 20 | - | - | - | pentakis-dodécaèdre (triangle isocèle) | |
| icosidodécaèdre | 30 | 60 | 32 | 20 | - | 12 | - | - | - | - | triacontaèdre rhombique (losange) | |
| petit rhombicosidodécaèdre | 60 | 120 | 62 | 20 | 30 | 12 | - | - | - | - | hexécontaèdre deltoïdal (cerf-volant) | |
| grand rhombicosidodécaèdre | 120 | 180 | 62 | - | 30 | - | 20 | - | 12 | - | disdyakis-triacontaèdre(triangle) | |
| snub dodécaèdre | 60 | 150 | 92 | 80 | - | 12 | - | - | - | - | hexécontaèdre pentagonal (pentagone) | |
| prismes réguliers (ordre n ≥ 3) | 2n | 3n | n+2 | - | n | - | - | - | - | 2 | diamants réguliers (triangle isocèle) | |
| antiprismes réguliers (ordre n ≥ 3) | 2n | 4n | 2n+2 | 2n | - | - | - | - | - | 2 | antidiamants réguliers (cerf-volant) |
Dans "rhombicuboctaèdre" le préfixe "rhombi" indique que 12 faces carrées appartiennent aux faces d'un dodécaèdre rhombique (dual du cuboctaèdre).
De même les 30 faces carrées des "rhombicosidodécaèdres" appartiennent aux faces d'un triacontaèdre rhombique (dual de l'icosidodécaèdre).
Le grand rhombicuboctaèdre est aussi le cuboctaèdre tronqué ; de même le grand rhombicosidodécaèdre est l'icosidodécaèdre tronqué.
Généralisation à des polyèdres non convexes : f + s = a + 2 - 2t où t est le nombre de tunnels du polyèdre (son genre).
 |
 |
 |
|
On peut réaliser de jolis polyèdres de bien des manières : bois collé, fil de cuivre soudé, origami...
Le jeu de construction Geomag est une autre façon d'explorer le monde des polyèdres ; voici un bel exemple. | ||
| exemples : | cube : 8[2π-3(π/2)] = 4π
tétraèdre régulier : 4[2π-3(π/3)] = 4π dodécaèdre régulier : 20[360°-3x108°] = 720° |
cuboctaèdre : 12[2π-2(π/2+π/3)] = 4π
pyramide régulière pentagonale : 5[360°-(108°+2x60°)]+(360°-5x60°) = 720° dodécaèdre rhombique : 6[360°-4α]+8[360°-3(180°-α)] = 720° α=35.265...° |
Remarque sur la somme de tous les angles de faces : (Σαij)/2π = a-f = s-2 | ||
| exemples : | cube : 8[3(π/2)]/2π = 6 12-6 = 8-2 = 6
tétraèdre régulier : 4[3(π/3)]/2π = 2 6-4 = 4-2 = 2 dodécaèdre régulier : 20[3x108°]/360° = 18 30-12 = 20-2 = 18 |
cuboctaèdre : 12[2(π/2+π/3)]/2π = 10 24-14 = 12-2 = 10
pyramide régulière pentagonale : [5(108°+2x60°)+5x60°]/360° = 4 10-6 = 6-2 = 4 dodécaèdre rhombique : [6x4α+8x3(180°-α)]/360° = 12 24-12 = 14-2 = 12 |
La convexité est une notion assez naturelle. Sans en donner une définition explicite, il est facile de reconnaître un polyèdre convexe : toutes ses "vraies diagonales" (segments joignant deux sommets n'appartenant pas à une même face) sont à l'intérieur.
Condition de Minkowski : Soit u1, u2, ... uk des vecteurs unitaires qui engendrent l'espace, et a1, a2, ... , ak des nombres positifs. Alors il existe un polyèdre convexe (unique à translation près) dont les vecteurs unitaires normaux aux faces sont u1, u2, ... uk et les aires des faces correspondantes a1, a2, ... , ak si et seulement si a1 u1 + ... + ak uk = 0 (condition pour les polytopes convexes)
On peut évidemment s'intéresser à une catégorie particulière de polyèdres convexes, par exemple :
• les polyèdres à faces régulières : on connaît les platoniciens, les archimédiens, les prismes et antiprismes ;
les autres sont les 92 solides de Johnson (pyramides, diamants, coupoles... assemblages des précédents),
• les différents types d'hexaèdres, moins faciles à trouver que les tétraèdres (tous ont quatre faces triangulaires) ou les pentaèdres (dont les deux types sont les pyramides à base quadrilatère et les "toits" formés de trois quadrilatères et deux triangles),
• les deltaèdres dont toutes les faces sont des triangles équilatéraux,
• les polyèdres avec un nombre donné de faces,
• les pyramides qui permettent de réaliser des puzzles,
• les tectoèdres qui s'obtiennent en pratiquant des coupes successives dans des tétraèdres,
• les polyèdres de Waterman dont les sommets sont les centres de sphères d'un empilement cubique compact,
• les zonoèdres dont toutes les faces ont un centre de symétrie,
• les polyèdres zoniques avec des "zones" de parallélogrammes,
• les polyèdres rhombiques dont toutes les faces sont des losanges,
• les polyèdres avec des faces régulières et des losanges d'or,
• les polyèdres avec des faces régulières et des trapèzes 1:1:1:2,
• les polyèdres avec des faces régulières et des losanges particuliers (R2 ou losanges d'or),
• les polyèdres sphériques (dômes),
• les polyèdres de Goldberg,
• les 144 polyèdres obtenus par troncatures d'arêtes du cube,
• les symétroèdres : polyèdres convexes avec "peu" de types de faces, dont "beaucoup" régulières (document pdf en anglais),
• des exemples simples de polyèdres canoniques avec un des 17 types de symétrie,
• . . .
De nombreux autres exemples ont d'intéressantes propriétés : l'alvéole d'abeille, les cristaux, les fullérènes (molécules de carbone), les pierres précieuses taillées . . .

Les polyèdres avec seulement des faces pentagonales et hexagonales ont toujours douze faces pentagonales.
Les fullérènes ont de telles structures, par exemple le C60 (icosaèdre tronqué avec 20 faces hexagonales) et le C80 (triacontaèdre rhombique tronqué avec 30 faces hexagonales non régulières).
Les paralléloèdres de Fedorov vérifient trois conditions : les faces sont deux à deux opposées et parallèles, chaque arête appartient à un ensemble d'arêtes parallèles (trois ou six arêtes), et ils pavent l'espace en n'utilisant que des translations. Il n'y en a que cinq, à transformations affines près : l'octaèdre tronqué, le dodécaèdre rhombique allongé, le dodécaèdre rhombique, le prisme hexagonal (non nécessairement régulier ou droit) et le cube (donc aussi tous les parallélépipèdes) ; en partant des six ensembles de six arêtes parallèles de l'octaèdre tronqué, on supprime, par étapes, des ensembles d'arêtes parallèles pour obtenir les autres et arriver aux trois ensembles de quatre arêtes du cube.
L'enveloppe convexe d'un polyèdre P est l'unique plus petit polyèdre convexe contenant P.
|
• coupes dans un cube (The Mathematical Gazette)
Dans un cube de côté 1 on coupe tous les tétraèdres "coin de cube" du type indiqué sur le dessin (si on prend la coupe comme base, les trois arêtes latérales sont deux arêtes et une demi-arête du cube). Décrire et dessiner le polyèdre restant, puis calculer son volume. |
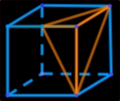 |
| références : |
• Twenty Proofs of Euler's Formulæ sur "The Geometry Junkyard" (en anglais)
• Si vous désirez manipuler, modifier l'aspect, colorier selon vos goûts, et imprimer les patrons de 147 polyèdres convexes, alors POLY est le programme qu'il vous faut ! • Avec STELLA vous pourrez accéder à une infinité de polyèdres (convexes ou non) et en créer de nouveaux. Un "must" pour ceux qui désirent plonger dans le monde des polyèdres ! • Un bel ensemble de 30 polyèdres convexes en bois. • Quelques résultats concernant les polyèdres convexes par Gérard P. Michon (en anglais). |
page accueil
 |
polyèdres convexes - polyèdres non convexes - polyèdres intéressants - sujets connexes | avril 1999 mis à jour 275-05-2023 |