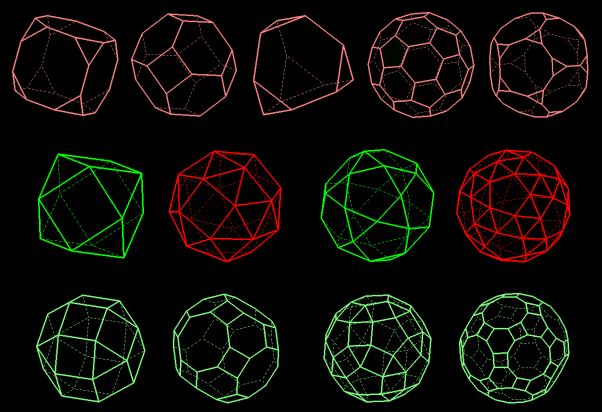
Ces polyèdres semi-réguliers convexes ont des faces régulières (de deux ou trois types) ; leurs sommets sont superposables (mais pas réguliers) et cosphériques (sphère circonscrite) ; leurs arêtes ont même longueur.
Onze de ces treize polyèdres semi-réguliers de première espèce peuvent être obtenus par troncatures des polyèdres réguliers (les deux grands rhombi... nécessitent des troncatures successives). Les deux derniers, les "snubs" (en rouge sur la figure) ne peuvent être obtenus par cette méthode ; ils n'ont pas de plan de symétrie, et existent donc dans les deux orientations (images dans un miroir).

Chaque dessin propose un lien vers un pop-up applet (davantage sur les caractéristiques des polyèdres semi-réguliers).
|
|
En coupant les "coins" d'un cube ou d'un octaèdre régulier en passant par les milieux des arêtes (troncature par les sommets), on obtient un cuboctaèdre dont les sommets sont les sommets de quatre hexagones réguliers.
Une telle troncature d'un dodécaèdre régulier ou d'un icosaèdre régulier conduit à un icosidodécaèdre dont les sommets sont les sommets de six décagones réguliers. |
|
On obtient le snub cube en effectuant une similitude (réduction et rotation de centre le centre d'une face) sur chaque face du cube de façon à créer des anneaux de triangles équilatéraux autour des nouveaux carrés. Il n'y a plus de plan de symétrie, donc ce polyèdre est chiral (ses deux formes sont images dans un miroir).
On obtient de même le snub dodécaèdre à partir du dodécaèdre régulier.
|
|
|
|
|
|
|

L'icosaèdre tronqué est bien connu des amateurs de football. (les bandes noires correspondent aux arêtes d'un icosidodécaèdre) à droite, cérémonie d'ouverture de la coupe du monde 2014 |
 |
 |
|
|
L'icosaèdre tronqué est aussi la structure du fullérène le plus connu, le C60 (60 atomes de carbone avec des liaisons simples selon les côtés des pentagones et doubles entre les pentagones).
| ||
Tous les solides archimédiens vérifient (2π-A) s = 4π où A désigne la somme des angles en un sommet et s le nombre de sommets.
Une curiosité (Pugh - 1976) : tous les solides archimédiens peuvent être circonscrits par un tétraèdre régulier de manière à ce que quatre de leurs faces appartiennent aux faces de ce tétraèdre.
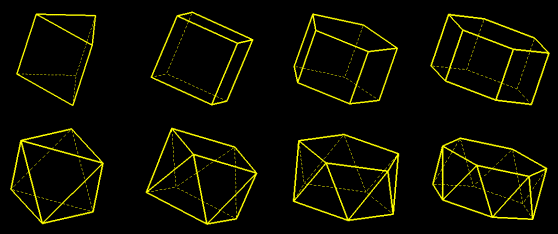
Le prisme carré est le cube ; l'antiprisme triangulaire est l'octaèdre régulier.
La hauteur d'un antiprisme régulier d'ordre n (distance des bases) et d'arête a vaut (a/2)√(3-tan(π/2n)).
La hauteur de l'antiprisme pentagonal est égale au rayon du cercle circonscrit au pentagone.
En assemblant deux pyramides pentagonales sur les bases d'un antiprisme pentagonal on obtient un icosaèdre régulier.
page accueil
 |
polyèdres convexes - polyèdres non convexes - polyèdres intéressants - sujets connexes | décembre 1998 mis à jour 30-06-2005 |