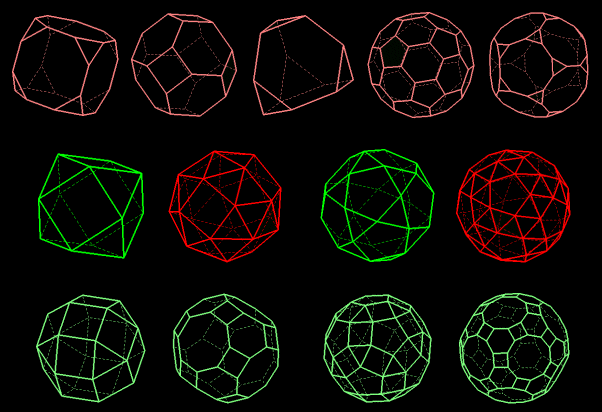
The faces of these semi-regular polyhedra are regular polygons (of two or three types) ; their vertices are superimposable (but not regular) and lay on a sphere (circumscribed sphere); their edges have same length.
Eleven of these thirteen semi-regular polyhedra of the first kind can be obtained by successive truncations of the regular polyhedra (the two great rhombi... need successive truncations). The last two, the snubs (in red on the picture), can't be obtained using this method ; they have no plane of symmetry, thus they exist in two orientations (mirror images).

Each drawing provides a link to a popup applet (more about the characteristics of the semi-regular polyhedra).
|
|
By cutting the "peaks" of a cube or of a regular octahedron, using the midpoints of the edges, (truncation by the vertices), we get a cuboctahedron whose vertices are the vertices of four regular hexagons.
Applying such a truncation to a regular dodecahedron or a regular icosahedron leads to an icosidodecahedron whose vertices are the vertices of six regular decagons. |
|
We get the snub cube by performing a similarity (reduction and rotation with centers the center of a face) on each face of the cube in order to create rings of equilateral triangles around the new squares. There is no plane of symmetry, thus this polyhedron is chiral (its two forms are mirror images).
In the same way we get the snub dodecahedron from the regular dodecahedron.
|
|
|
|
|
|
|

The truncated icosahedron is well known by soccer amateurs. (the black strips correspond to the edges of an icosidodecahedron) on the right, opening ceremony of the world cup 2014 (São Paulo - Brazil) |
 |
 |
|
|
The truncated icosahedron is also the structure of the best known fullerene, the C60 (60 atoms of carbon with simple links along the pentagons' sides and double links between the pentagons).
| ||
All the Archimedean solids satisfy (2π-A) v = 4π where A is the sum of face's angles at a vertex and v the number of vertices.
A curiosity (Pugh - 1976): the Archimedean solids can all be circumscribed by a regular tetrahedron so that four of their faces lie on the faces of that tetrahedron.
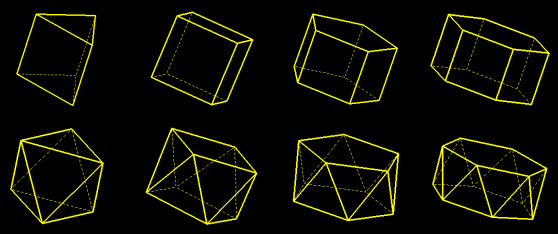
The square prism is the cube; the triangular antiprism is the regular octahedron.
The height of a regular antiprism of order n (distance of the bases) and edge a is (a/2)√(3-tan(π/2n)).
The hight of the pentagonal antiprism is equal to the radius of the circle circumscribed to the pentagon.
By assembling two pentagonal pyramids on the bases of a pentagonal antiprism we get a regular icosahedron.
home page
 |
convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects | December 1998 updated 30-06-2005 |