l'alvéole d'abeille
Le gâteau de cire construit par les abeilles pour y déposer leur miel est formé par deux couches d'alvéoles opposées par leur fond.
Une alvéole ressemble à un prisme droit à base hexagonale régulière (l'ouverture), mais le fond est un assemblage non plan de trois losanges identiques qui appartiennent chacun à deux alvéoles opposées.
Aristote avait déjà remarqué la forme hexagonale des alvéoles, et Pappus en a fait la première étude géométrique. Ce n'est qu'au 18e siècle qu'on remarqua la forme du fond, et en 1712 que Maraldi détermina expérimentalement l'angles des losanges : 70°32'. Réaumur soupçonna les abeilles de construire le fond de façon à n'utiliser qu'un minimum de cire. Koenig traita le problème par le calcul différentiel et trouva une valeur légèrement différente. L'écart entre les deux valeur n'était que de 6'... jusqu'à ce que Mac Laurin prouve en 1739 que Koenig avait commis une erreur dans ses calculs ; les valeurs de Maraldi étaient exactes !
|
 |
|
L'étude de l'alvéole, dont le patron peut être construit à la règle et au compas, révèle quelques autres propriétés remarquables :
• les trois diagonales concourantes au sommet commun des trois losanges sont deux à deux perpendiculaires,
• les plans de deux faces quelconques ayant une arête en commun forment un dièdre d'angle 120°.
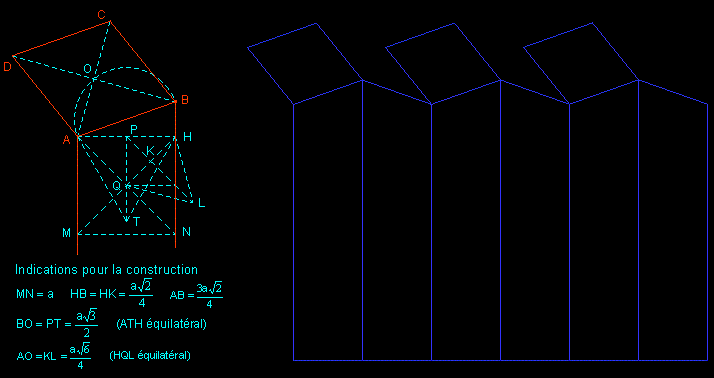
| Les propriétés ci-dessus sont celles du dodécaèdre rhombique ; on peut donc obtenir simplement une alvéole en étirant un dodécaèdre rhombique : il suffit ensuite de couper (orthogonalement à son axe) une des "extrémités" de ce dodécaèdre rhombique allongé qui pave l'espace. |
|
| référence : |
Géométrie de l'espace et du plan de Yvonne et René Sortais (éditions Hermann - 1988) pages 387-394 |



