the cell of a honeycomb
The honeycomb build by the bees to lay down their honey is formed by two layers of cells opposite by their bottom.
An alveolus looks like a right prism with a regular hexagonal base (the opening), but the bottom is an non flat assembling of three identical rhombuses which belong each to two opposite alveolus.
Aristotle had noticed the hexagonal form of the alveolus, and Pappus made it's first geometrical study. It's only during the 18th century that the form of the bottom has been noticed, and in 1712 Maraldi experimentally worked out the angle of the rhombus: 70°32'. Réaumur suspected the bees to build the bottom in order the use only the minimum of wax. Koenig dealt with the problem, using differential calculus, and found a slightly different value. The difference between the two values was only 6'... until Mac Laurin proved in 1739 that Koenig made a mistake in his calculations; the value found by Maraldi was exact!
|
 |
|
The study of the alveolus, whose template can be constructed with ruler and compasses, reveals other outstanding properties:
• the three diagonals which converge on the vertex common to the three rhombuses are two by two perpendicular,
• the planes of two faces with an edge in common have a dihedral angle of 120°.
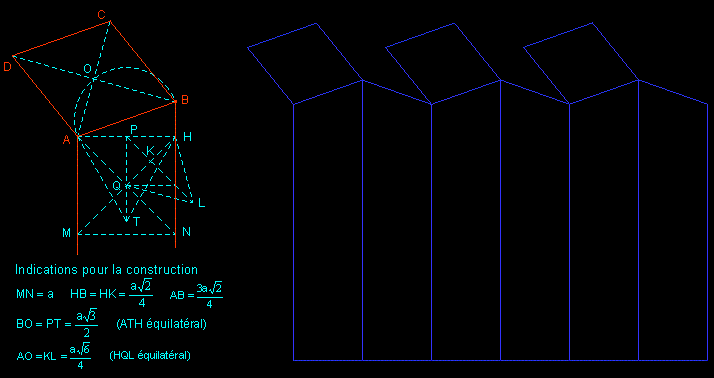
| The properties above are those of the rhombic dodecahedron; thus one can easily build an alveolus by stretching a rhombic dodecahedron: then just cut (orthogonally to its axis) one "end" of this elongated rhombic dodecahedron which fills the space. |
|
| reference: |
Géométrie de l'espace et du plan (in French) by Yvonne and René Sortais (Hermann - 1988) pages 387-394 |



