tectoèdres et tas de sable

les tectoèdres  ( Roger Iss )

Un tectoèdre (du latin tectum = toit) est un polyèdre convexe dont une face, la base, est adjacente à toutes les autres faces, et dont tous les sommets sont d'ordre 3 (cette seconde condition évite des cas particuliers comme les pyramides).
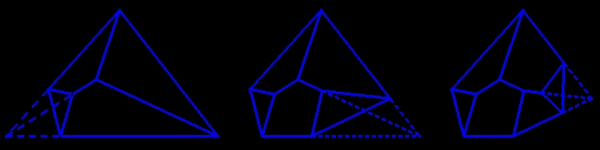
On peut facilement réaliser de tels polyèdres par troncatures successives d'un tétraèdre : on coupe un petit tétraèdre défini par un sommet de base et les trois autres choisis sur les trois arêtes issues du premier. À chaque étape la base gagne un sommet.
Une vue de dessus suffit donc pour représenter un tectoèdre d'ordre n (la base est un n-gone) qui a :
  • n faces latérales que l'on appelle simplement faces,
  • deux types de sommets : les n de la base et les autres que l'on appelle simplement sommets,
  • trois types d'arêtes : les n côtés de la base, les n arêtes latérales (issues des sommets de base),
      et les autres (d'extrémités deux sommets) que l'on appelle arêtes faîtières.
troncatures

trois troncatures successives d'un tétraèdre
conduisent à des tectoèdres d'ordres 4, 5 et 6,
avec une, deux et trois arêtes faîtières

à droite une animation LiveGraphics3D avec ces trois troncatures

propriétés :
tectoèdre d'ordre n
(la base est un n-gone) 		• le tétraèdre est un cas particulier : un seul sommet, pas d'arête faîtière,
• tout pentaèdre est un tectoèdre d'ordre 4, et il l'est de trois manières (trois faces sont quadrangulaires),
• le nombre de faces triangulaires est compris entre 2 et n/2, et deux telles faces ne sont pas adjacentes,
• il y a (n-2) sommets  et (n-3) arêtes faîtières,
• pour tout n il existe un tectoèdre à deux bases (il a la forme d'un "coin" avec deux n-gones),
• tout tectoèdre sans arête faîtière  parallèle à la base est issu (par troncatures successives) d'un tétraèdre, sinon il est issu d'un pentaèdre avec trois arêtes parallèles.
exercices :

solutions   		• À partir d'un polygone de base construire la vue de dessus d'un tectoèdre.
   Indication : dessiner un tétraèdre dont le tectoèdre est issu (voir "coupons un tétraèdre").
   Peut-on choisir le sommet du tétraèdre en dehors du polygone de base ?
• Construire le patron d'un tel tectoèdre, puis le réaliser.

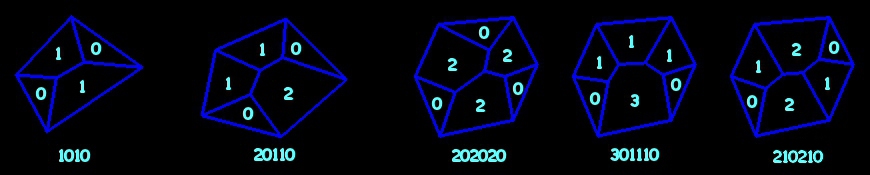
classification des tectoèdres

On s'intéresse ici à la topologie, c'est à dire à la nature et l'agencement des faces. Roger Iss attribue à chaque tectoèdre une formule  en associant à chaque face le nombre d'arêtes faîtières  parmi ses côtés. On peut ainsi déterminer les différentes classes de tectoèdres par récurrence sur l'ordre. À chaque troncature correspond une manipulation numérique facile à programmer sur un ordinateur. Pour davantage de détails, voir le document en référence.

On peut aussi transformer la vue de dessus par "dualité" : dans chaque face latérale on choisit un point arbitraire, puis on relie les points correspondant à des faces adjacentes (à chaque arête latérale ou faîtière  correspond alors un segment). On obtient ainsi un n-gone - que l'on peut choisir convexe - triangulé en (n-2) triangles par (n-3) diagonales.
On retrouve la formule  en associant à chaque sommet le nombre des diagonales qui en sont issues. Une troncature correspond à l'augmentation du n-gone par un triangle (le côté commun est alors une diagonale du (n+1)-gone). 	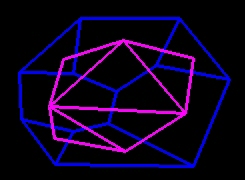	image duale

Le nombre de triangulations d'un n-gone étant connu, on peut calculer le nombre Tn de classes de tectoèdres d'ordre n ; il croît très rapidement avec n.
     T4 = 1    T5 = 1    T6 = 3    T7 = 4    T8 = 12    T9 = 27    T10 = 82   ...   T15 ≈ 25000   ...   T20 > 107   ...
Voici des représentations des tectoèdres d'ordres 4, 5 et 6 avec les formules  associées :

tectoèdres

des tas de sable  ( Francis Jamm )

Des tas de sable ? quel rapport avec les tectoèdres ?
Si on fait tomber du sable sur une plaque plane horizontale on finit par produire un "tas maximum" sur lequel on ne peut plus ajouter de sable (il glisse jusqu'au bord de la plaque et tombe). Voici quelques propriétés de ces tas :
• la forme du tas ne dépend que de la plaque (un polygone régulier produit une pyramide régulière, sur un disque apparaît un cône...),
• pour une plaque convexe la surface du tas fait un angle constant d'environ 30° à 35° avec la plaque (selon la nature du sable),
• les grains de sable glissent vers le bord de la plaque le plus proche, donc les points des arêtes faîtières  du tas sont équidistants de deux bords.

On peut évidemment utiliser des plaques de formes diverses (bords arrondis, non convexes, avec des trous...) qui conduisent à des tas aux formes parfois surprenantes (voir les sites des lycées Lavoisier et Alain Borne en référence), mais nous ne nous intéressons ici qu'aux plaques polygonales convexes qui produisent... des tectoèdres ! (au sens général, sans la contrainte sur l'ordre des sommets)
Voici quelques exemples avec des quadrilatères et des pentagones comme polygones de base :

quadrilatère

parallélogramme (pentaèdre à arêtes parallèles)
(arête faîtière = différence des arêtes des bases)

quadrilatère circonscrit à un cercle

pentagone

pentagone avec trois bissectrices concourantes

pentagone circonscrit à un cercle

La troisième propriété ci-dessus implique qu'une arête faîtière  appartienne au plan bissecteur du secteur de la base défini par les deux bords concernés ; sur la vue de dessus c'est un segment de la bissectrice du secteur. La deuxième propriété ajoute évidemment une contrainte supplémentaire.
Un polygone qui admet un cercle inscrit (⇔ ses bissectrices intérieures sont concourantes) produit une pyramide et le centre du cercle est la projection orthogonale du sommet. Plus généralement, si au moins trois bissectrices de la base sont concourantes, alors le nombre d'arêtes faîtières  diminue et le nombre de faces triangulaires augmente (il y en a alors qui sont adjacentes).

références : •  Les tectoèdres  par Roger Iss (Bulletin de l'APMEP n° 402, février 1996) - pdf (120 Ko)
•  La géométrie des tas de sable ou les surfaces "d'égale pente"  par Robert March (Bulletin de l'APMEP n° 442, septembre 2002)
•  Sable et mathématiques  par Roger Iss (L'Ouvert n° 41, décembre 1985  &  n° 42, mars 1986) - PDF (540 Ko)
•  La géométrie des tas de sable  Tangente n°94, septembre-octobre 2003  &  Tangente sup n°21, octobre 2003
•  le site de Roger Iss  Une curieuse famille de polyèdres : les tectoèdres
•  Les tas de sable au club... scientifique  par Francis Jamm (lycée Lavoisier, Mulhouse) - PDF-1 (1,2 Mo)  -  PDF-2 (1,2 Mo)
•  le site du club scientifique du lycée Lavoisier de Mulhouse
•  des pages du site du lycée Lavoisier de Mulhouse
•  une page de mathcurve.com  surfaces d'égale pente
•  La science des châteaux de sable  (blog de David Louapre)

page accueil
anglais 		polyèdres convexes - polyèdres non convexes - polyèdres intéressants - sujets connexes avril 2008
mis à jour 23-04-2008