tectohedra and sand heaps

the tectohedra   ( Roger Iss )

A tectohedron (from the Latin tectum = roof) is a convex polyhedron where one face, the base, is adjacent to all the other faces, and whose vertices are all of order 3 (this second condition avoids special cases like the pyramids).
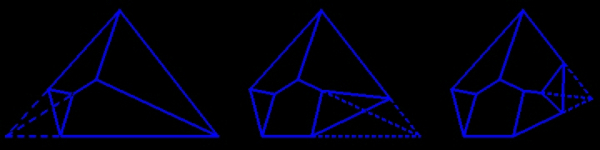
Such polyhedra are easy to build by successive truncations of a tetrahedron: cut a small tetrahedron defined by one vertex of the base and the three others chosen on the three edges starting at the first. At each step the base gets a new vertex.
A top view thus suffice to represent a tectohedron of order n (the base is a n-gon) which has:
  • n lateral faces which we call simply faces,
  • two types of vertices: the n base's vertices and the others which we call simply vertices,
  • three types of edges: the n base's sides, the n lateral edges (starting at the base's vertices)
      and the others (with ends at two vertices) which we call ridge-pole edges.
truncations

three successive truncation of a tetrahedron lead to tectohedra of orders 4, 5 and 6,
with one, two and three ridge-pole edges

on the right a LiveGraphics3D animation with these three truncations

properties:
tectohedron of order n
(the base is a n-gon) 		• the tetrahedron is a special case: only one vertex, no ridge-pole edges,
• every pentahedron is a tectohedron of order 4 and it is so in three different ways (three quadrilateral faces),
• the number of triangular faces is contained between 2 and n/2 and two such faces are not adjacent,
• there are (n-2) vertices  and (n-3) ridge-pole edges,
• for every n there is a tectohedron with two bases (it looks like a "wedge" with two n-gons),
• every tectohedron without ridge-pole edge  parallel to the base stems (by successive truncations) from a tetrahedron, otherwise it stems from a pentahedron with three parallel edges.
exercises:

solutions   		• Starting from a base polygon construct the top view of a tectohedron.
   Indication: draw a tetrahedron from which the tectohedron stems (see "cutting a tetrahedron").
   Can the vertex of the tetrahedron be chosen outside of the base polygon?
• Construct the net of such a tectohedron, then build it.

classification of the tectohedra

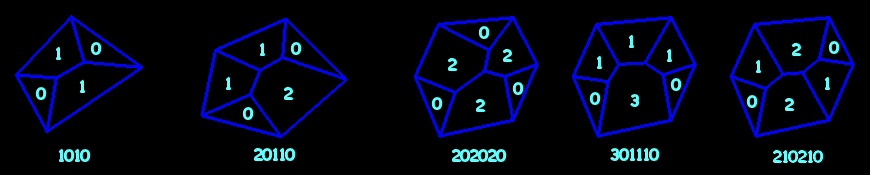
Here we are interested in the topology, that means in the nature and the layout of the faces. Roger Iss assigns a formula  to each tectohedron by associating to each face the number of ridge-pole edges  among its sides. So one can determine the different classes of tectohedra by recurrence on the order. To each truncation corresponds a numeric manipulation easy to program on a computer. For more details see the document in reference.

The top view can be transformed by "duality": in each lateral face chose an arbitrary point, then link the points corresponding to adjacent faces (to each lateral or ridge-pole edge  corresponds then a line segment). Thus we get a n-gon - which can be chosen convex - triangulated in (n-2) triangles by (n-3) diagonals
We find the formula  by associating to each vertex the number of diagonals which start from it. A truncation corresponds to the augmentation of the n-gon by a triangle (the common side is then a diagonal of the (n+1)-gon). 	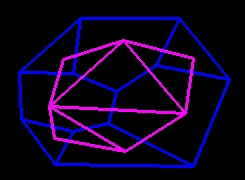	image duale

The number of triangulations of a n-gon is known, thus the number Tn of classes of order n tectohedra can be computed; it grows very quickly with n.

     T4 = 1    T5 = 1    T6 = 3    T7 = 4    T8 = 12    T9 = 27    T10 = 82   ...   T15 ≈ 25000   ...   T20 > 107   ...


Here are representations of the tectohedra of orders 4, 5 and 6 with the associated formulæ :

tectoèdres

sand heap  ( Francis Jamm )

Sand heaps? what connection with tectohedra?
If one pours sand on an horizontal sheet it ends with a "maximum heap" on which no sand can be added (it glides to the edge and falls). Here are a few properties of these heaps:
• the form of the heap depends only on the sheet (a regular polygon produces a pyramid, on a disk appears a cone...),
• for a convex sheet the angle between the sheet and the heap's surface is constant around 30° to 35° (depending on the nature of the sand),
• the sand grains slide to the nearest edge of the sheet, thus the points of the ridge-pole edges  of the heap are equidistant from two edges.

Of course sheets of different shapes can be used (round edges, non convex, with holes...); they lead to heaps with sometimes surprising shapes (see the web sites of Lavoisier and Alain Borne secondary schools in reference), but here we are only interested in convex polygonal sheets which produce... tectohedra! (in general meaning, without the constraint on the order of the vertices).
Here are a few examples with quadrilaterals and pentagons as base polygons:

quadrilateral

parallelogram (pentahedron with parallel edges)
(ridge-pole edge = difference between the base's edges)

quadrilateral circumscribed to a circle

pentagon

pentagon with three concurrent bisectors

pentagon circumscribed to a circle

The third property above implies that a ridge-pole edge  belongs to the bisector plane of the base's sector defined by the concerned edges; on the top view it is a bisector's segment of the sector. The second property adds of course a supplementary constraint.
A polygon which has an inscribed circle (⇔ its interior bisectors are concurrent) produces a pyramid and the center of the circle is the orthogonal projection of the apex. More generally if at least three bisectors of the base are concurrent then the number of ridge-pole edges  decreases and the number of triangular faces increases (there are then adjacent ones).

references: •  Les tectoèdres  by Roger Iss (Bulletin de l'APMEP n° 402, February 1996) - pdf (120 Kb, in French)
•  La géométrie des tas de sable ou les surfaces "d'égale pente"  by Robert March (Bulletin de l'APMEP n° 442, September 2002, in French)
•  Sable et mathématiques  by Roger Iss (L'Ouvert n° 41, December 1985  &  n° 42, March 1986) - PDF (540 Kb, in French)
•  La géométrie des tas de sable  (Tangente n°94, September-October 2003  &  Tangente sup n°21, October 2003, in French)
•  the site by Roger Iss  Une curieuse famille de polyèdres : les tectoèdres  (in French)
•  Les tas de sable au club... scientifique  by Francis Jamm (lycée Lavoisier, Mulhouse) - PDF (1,2 Mb)  -  PDF-2 (1,2 Mb), both in French
•  the web site of the scientific club  of lycée Lavoisier in Mulhouse (France)
•  pages from the web site of lycée Lavoisier in Mulhouse  (in French & English)
•  a page from mathcurve.com  surfaces d'égale pente  (in French) La science des châteaux de sable  (blog of David Louapre, in French)

home page
French 		convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects April 2008
updated 23-04-2008