lest's construct tectohedra

The technique used for the construction of a tetrahedron can be used to construct a pentahedron with three parallel edges (the second polyhedron which produces tectohedra by truncations).
•   Each lateral face turns around its bases's side; two corresponding vertices are thus on a line perpendicular to this side.
•   The choice of one of the yellow points determines the hight of the polyhedron and permits to construct the others gradually.

nets

construction of a tectohedra of order 6

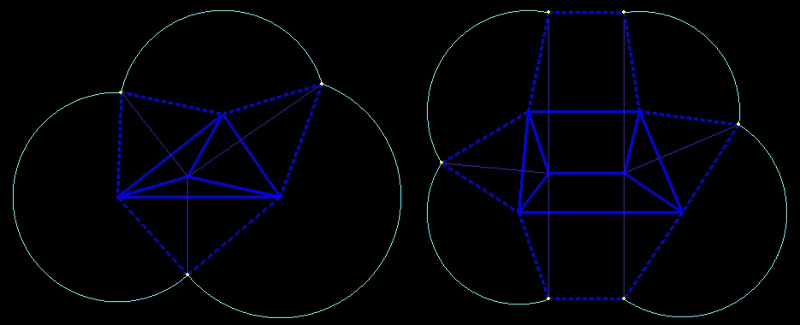
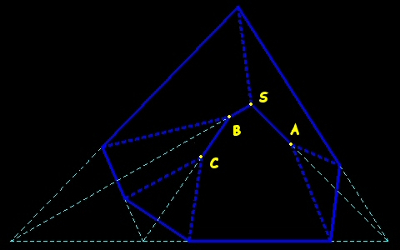
top view top view constructed starting from the base We start by inscribing the base in a triangle whose sides must contain three sides of the polygon; it is the base of a tetrahedron and we choose its apex S.
Here a lateral edge of the tetrahedron is also one for the tectohedron.
The vertices A and B, chosen on the two other lateral edges of the tetrahedron starting at S, define two ridgepole edges.
We can now draw the cut through A.
The drawing of the cut through B allows us to place the vertex C, and to draw the cut through C.

The method consist thus to start from the apex of the tetrahedron and to choose gradually the other vertices which define the ridgepole edges. At each stage we can draw the cut through the last chosen vertex.
remark: the vertex S of the tetrahedron can be chosen everywhere in the plane, including the sides of the base.
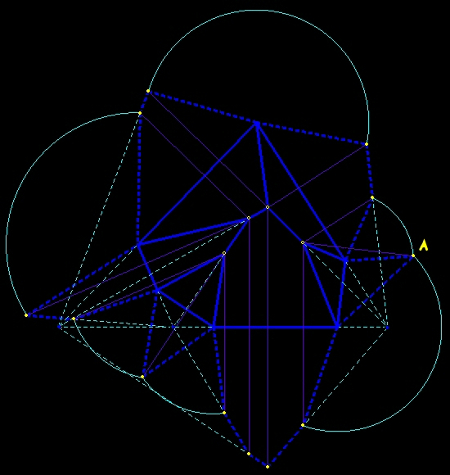
patron net constructed starting from the top view The points to be constructed (in yellow) permit to draw the sides of the lateral faces (dashed line segments in blue).

Properties to be respected during the construction:
• Each point to be constructed lays on the line perpendicular to the bases's side and going through the correspondent vertex (the face turns around the bases's side).
• Two line segments corresponding to the same edge have same length.
• The alignments are preserved: a ridgepole edge line goes through the intersection of two side lines of the base, the same must hold for the corresponding segment lines.

remark: the choice of the first point (for example A) determines the hight of the tectohedron, thus it must be chosen at a distance from the base far greater as the one of the corresponding vertex; we construct the other points gradually (in any direction).

The construction becomes more tricky if, on the top view, the vertex S of the tetrahedron has been chosen outside of the base polygon.

home page
French 		convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects April 2008
updated 20-04-2008