a few outstanding tetrahedra
A tetrahedron ("four faces") is the most simple of the polyhedra: its four vertices define four triangular faces assembled with six edges.
The regular tetrahedron and the regular right-angled tetrahedron can easily be obtained from a cube.
|
|
|
|
|
| a regular tetrahedron |
a regular tri-right-angled tetrahedron |
a diamond (compound
of these two regular pyramids) |
Schläflis' birectangular tetrahedron
(four rectangular faces) |
|
We can do so using a rectangular parallelepiped to obtain other types of tetrahedra. |
|
|
|
|
an equifacial tetrahedron
(disphenoid) |
a tri-right-angled tetrahedron |
an equifacial tetrahedron
with isosceles faces
(tetragonal disphenoid) |
an other tetrahedron with
right-angled faces (non equifacial) |
Here are two other interesting tetrahedra defined in a cube (1/24 of the cube's volume):
• if we cut out the first (blue) along each of the twelve edges of a cube it remains a Kepler star (see puzzles),
• 6 of the second (magenta) can build an oblate rhombohedron, 8 an octahedron (longest edge in common), 24 a cube (two along each edge), 6×8=48 a rhombic dodecahedron (six octahedra with a common vertex); 12 pairs (bipyramids) with a common vertex build a stellated rhombic dodecahedron. |
|
See also the Hill's tetrahedra (paving of the space, decomposition).
a few properties of tetrahedra
- It might be useful to remind that the tetrahedron is the "simplest" polyhedron: one can't have less than 4 faces, 4 vertices and 6 edges (with 3 vertices and 3 sides, the triangle is the "simplest" polygon).
A tetrahedron has no diagonal (the six segments joining two of the four vertices are edges).
The volume V of a tetrahedron is the third of the volume of the prism with same base of area A and same height h: V=(A×h)/3
(see exercise at the end of the page).
Each face of the tetrahedron may obviously be used as base, like each side of a triangle may be used to compute its area: A=(l×h)/2.
- Generalization of the "centers" of a triangle: a tetrahedron is inscribed in a sphere (circumsphere) and has an inscribed sphere (insphere, tangent to its faces).
The four perpendiculars to the faces' planes and going through the centers of the circumcircles of the faces converge at the center of the tetrahedron's circumsphere.
The center I of the sphere inscribed in a tetrahedron (ABCD) verifies I = (Sa/S)A+(Sb/S)B+(Sc/S)C+(Sd/S)D where Sa, Sb, Sc and Sd are the areas of the faces opposite to A, B, C and D respectively, and S=Sa+Sb+Sc+Sd ; its radius r verifies r=3V/S (by decomposing the tetrahedron into four tetrahedra with common vertex I we get V=Sr/3 ) and 1/r = 1/h1+1/h2+1/h3+1/h4 where the hi are the altitudes of the tetrahedron and V its volume.
In a triangle ABC the incenter I verifies I = (a/p)A+(b/p)B+(c/p)C where a, b and c are the lengths of the sides opposite to A, B and C respectively, and p=a+b+c the perimeter of the triangle; its radius r verifies r=2S/p and 1/r = 1/h1+1/h2+1/h3 where the hi are the altitudes of the triangle and S its area.
The computation of the centers and the radii is not easy for a tetrahedron without special properties. Of course in the case of the regular tetrahedron things are simple (see exercise at the end of the page).
Remarks: besides the insphere there are also four exspheres, like there are three excircles in a triangle.
Only the Crelle's tetrahedra have a mid-sphere (tangent to the six edges).
This figure may be dynamically modified by moving three of the tetrahedron's vertices (red points) with the mouse pointer. |
|
The center of gravity (centroid or isobarycentre of the vertices) is the point of concurrency of the four segments joining each vertex to the centers of gravity of the opposite face; it lays on the quarter of each of these segments, starting from the face.
Generally a tetrahedron has no orthocentre (see orthocentric tetrahedra).
- Generalization of the Heron formula (volume of the tetrahedron): for a tetrahedron of opposite edges a and a', b and b', c and c'
V²=[4a²b²c²-a²(b²+c²-a'²)²-b²(c²+a²-b'²)²-c²(a²+b²-c'²)²+(b²+c²-a'²)(c²+a²-b'²)(a²+b²-c'²)]/144
The volume of ABCD is the sixth of the volume of the parallelepiped constructed from the edges AB, AC and AD (half base area, same height). Using the coordinates of the vertices A(ax,ay,az), B(bx,by,bz), C(cx,cy,cz) and D(dx,dy,dz), it expresses itself with the help of a determinant:
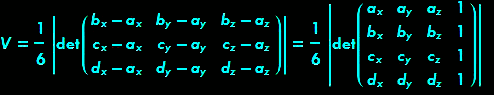 |
 |
triangle's area by Heron: sides a, b and c, A²=s(s-a)(s-b)(s-c) where s=(a+b+c)/2 is the half-perimeter.
area of a convex quadrilateral: sides a, b, c and d, A²=(s-a)(s-b)(s-c)(s-d)-abcd×cos(S)²
where s=(a+b+c+d)/2 is the half-perimeter and S half the sum of two opposite angles; for cyclic quadrilaterals cos(S)=0
- Every tetrahedron can be "inscribed" in a parallelepiped of volume three times that of the tetrahedron.
proof: the computation is easy in the case of a regular tetrahedron inscribed in a cube with edge 1 (each of the four tri-right-angled tetrahedra has a volume of 1/6; thus it remains 1/3 for the regular tetrahedron).
Generalizing is easy: the four pyramids have the same volume (same height, that of the parallelepiped, and bases with same area, half of that of the parallelepiped's base).
The edges of the tetrahedron are six of the twelve diagonals of the parallelepiped's faces.
The six other diagonals of the parallelepiped's faces define a second tetrahedron with same volume. The union of these two tetrahedra is an "anti-parallelepiped" (distorted anticube).
This figure may be dynamically modified by moving the vertices of the tetrahedron (yellow points) with the mouse pointer.
The "f" key is a switch to display the faces or only the edges.
|
|
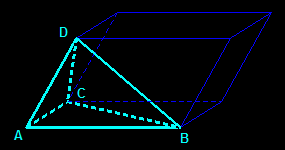
- First generalization of Varignon's theorem (skew quadrilateral):
the three segments joining the midpoints of opposite edges have same midpoint.
 |
In every quadrilateral (even non convex or crossed) the midpoints of the sides are the vertices of a parallelogram.
If the diagonals of the quadrilateral have same length (resp. are perpendicular) then we get a rhombus (resp. a rectangle).
Four points define three quadrilaterals (on the left diagram one is convex and the two others are crossed) whose three Varignon's parallelograms have same center (the common midpoint of their diagonals). In the second configuration the three quadrilaterals are non convex and non crossed.
In every quadrilateral the three segments joining the midpoints of opposite sides and the midpoints of the diagonals have same midpoint (Varignon's point).
The theorem remains true in space (right diagram); the four non coplanar points are then the vertices of a tetrahedron; we can see on the applet above that the common midpoint is the center of the parallelepiped.
See also Varignon's octahedron. |
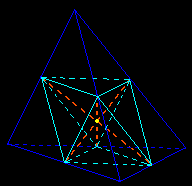 |
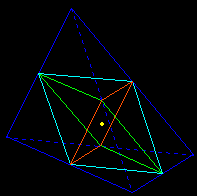
- Second generalization of Varignon's theorem (from the parallelogram to the parallelepiped):
the eight centroids of the faces of an octahedron are the vertices of a parallelepiped.
|
|
Here we really change dimension (move from the plane to the space):
• quadrilateral → octahedron
• midpoint of a side → centroid of a face
• parallelogram → parallelepiped
This figure may be dynamically modified by moving the vertices of the tetrahedron (yellow points) with the mouse pointer. The "f" key is a switch to display the faces of the octahedron.
Remark: The octahedron doesn't need to be convex: we may consider a crossed quadrilateral as two triangles which intersect on the same side of their common base; likewise a "crossed" octahedron may be seen as two "pyramids" which intersect on the same side of their common "base" (in fact it's a set of four non necessary coplanar points). By mowing the vertices of the octahedron we can test those configurations. |
- Generalization of Pythagoras theorem:in a right-angled tetrahedron (three right angles around one vertex) the square of the area of the non right-angled face is equal to the sum of the squares of the areas of the three other faces.
The computation is easy if you put the tri-right-angled vertex at the origin of an orthonormal system and the three others on the three axis. Pythagoras' theorem is used to compute the sides a, b and c of the non right-angled face and Heron's formula gives then its area.
The converse doesn't hold (a counter-example can be constructed using Minkowski's condition).
- A plane going through the midpoints of two opposite edges of a tetrahedron cuts the tetrahedron into two solids with same volume.
This interesting result deserves three proofs, all interesting:
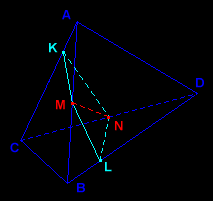
proof 1 (Vladimir Dubrovsky):
Let the midpoints M and N be taken on edges AB and CD, and let the other two vertices of the section (in light blue) be K (on AC) and L (on BD). A parallel projection of the whole construction along MN gives a parallelogram ACBD with center M=N in which AK/AC = BL/BD = k. One "half" of (ABCD) falls into the 4-sided pyramid (CKMLN) and the tetrahedron (LBCM), the other one into (DKMLN) and (KADM), and
vol(CKMLN)=vol(DKMLN) because they have same base and equal heights
vol(BCML) = vol (ADMK) = (k/2)×vol(ABCD) because bases(ABCD)/2 and heights(ABCD)×k
If K=A and L=B (or K=C and L=D) the two "halves" are tetrahedra with same volume: height(ABCD) and base(ABCD)/2
|
 |
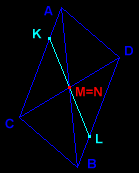 projection
projection |
proof 2 (Vladimir Dubrovsky) :
Consider the sections of (ABCD) parallel to AB and CD. They are parallelograms and the section cuts each of them into two equal symmetric parts (see the projection above). Then the equality of the volumes of the two pieces follows by "Cavalieri's Principle."
proof 3 (Georges Lion) :
Consider the symmetry with axis the line going through the midpoints of two opposite edges and parallel to the plane defined by the directions of these two edges; it preserves the tetrahedron and the section, and thus exchanges the two "halves". This symmetry is not orthogonal but it is an affine application whose associated linear application has 1 as determinant and thus preserves the volumes.
This figure may be dynamically modified by moving the five red points with the mouse pointer (the point which defines the section doesn't always follow the movement of the pointer!).
generalization: If a plane divides two opposite edges of a tetrahedron in a given ratio, then it divides the volume of the tetrahedron in the same ratio. (Altshiller-Court 1979, page 89) |
|
the equifacial tetrahedra (isometric faces)
⇔ the opposite edges have same length
⇔ the circumsphere and the insphere (tangent to the four faces) are concentric
⇔ at each vertex the sum of the face angles is 180°
• the four altitudes are equal
• the common perpendiculars to opposite edges come through the midpoints, are convergent and mutually perpendicular
• the isobarycentre G of the vertices is center of the circumscribed and inscribed spheres; the contact point of the insphere with a face is the circumcenter of that face
• the feet of the altitudes, the orthocentres of the faces and the midpoints of the altitudes lay on a sphere with center G
• the volume V is given by V²=(b²+c²-a²)(c²+a²-b²)(a²+b²-c²)/72 where a, b and c are the lengths of the pairs of opposite edges
examples: the regular tetrahedra, two of the tetrahedra above (see net below)
the orthocentric tetrahedra
⇔ two pairs of opposite edges are orthogonal (characteristic property)
⇔ three heights are concurrent (existence of an orthocenter H)
In fact we have a sufficient condition much more weak (Georges Lion).
If one of the altitude is secant with two others, not necessarily a priori at the same point, then the tetrahedron is orthocentric.
proof: For line AB to be orthogonal to line CD it is necessary and sufficient that h(A), altitude going through A, is secant with h(B).
Let us notice that generally h(A) and h(B) are orthogonal to CD without being parallels. We have then:
h(A) and h(B) are secant ⇔ h(A) and h(B) are coplanar ⇔ there is a plane going through A and B and perpendicular to CD.
If this condition is carried out the edges AB and CD are orthogonal and so are the edges AC and BD, thus the tetrahedron is orthocentric.
Remark: if h(A) and h(B) are secant then so are h(C) and h(D) but the tetrahedron ABCD is not necessarily orthocentric.
⇔ the foot of one altitude is orthocentre of the opposite face
⇔ a²+a'²=b²+b'²=c²+c'² where l and l' are the lengths of two opposite edges
• the three pairs of opposite edges are orthogonal
• the feet of the altitudes are orthocentres of the opposite faces
• the three common perpendicular to opposite edges are convergent in H
• the three segments joining the midpoints of opposite edges have same length
• the midpoints of the edges and the feet of the common perpendiculars to opposite edges lay on a sphere with center the isobarycentre G of the vertices (first Euler's sphere); the Euler's circles of the faces belong to this sphere
• G is midpoint of [OH] (Euler's line of the tetrahedron) where O is the center of the circumscribed sphere
• the perpendiculars to the faces on their centers of gravity are convergent in I on the Euler's line
• in a tetrahedron ABCD, the feet of the altitudes, the centers of gravity of the faces, and the points laying on the thirds of [HA], [HB], [HC] and [HD] lay on a sphere with center the midpoint of [HI] (second Euler's sphere)
• volume: V=(1/6)×l×l'×h where h is the length of the common perpendicular to two opposite edges of lengths l and l'
For any tetrahedron ABCD V=(1/6)×AB×CD×h×sin(x) where x is then angle (AB,CD)
The angle of two non coplanar lines is the one of their parallels going through some point (on the construction H is such a point).
reminder: construction of the common perpendicular Δ to two non coplanar lines D and D'
Let D" be the orthogonal projection of D' on the plane P going through D and parallel to D', and H its intersection point with D; Δ is the line perpendicular to P going through H.
This drawing is interactive: you may modify the tetrahedron by moving the red points B, C and D, and thus you can verify that the common perpendicular can be outside of the tetrahedron. |
|
examples: the regular tetrahedra, the trirectangle tetrahedra (the orthocentre is one vertex)
a construction of an orthocentric tetrahedron: let ABC be a triangle with orthocentre D' and let D be a point distinct from D' on the perpendicular to the plane of ABC going through D'.
the isodynamic tetrahedra
aa'=bb'=cc' where l and l' are the length of two opposite edges
⇔ the segments joining one vertex to the center of the circle inscribed in the opposite face are concurrent
Crelle's tetrahedra
a+a'=b+b'=c+c' where l and l' are the length of two opposite edges
⇔ there exists a sphere tangent to the six edges (mid-sphere)
example: the "4-ball tetrahedra"
a+a'=b+b'=c+c'=r1+r2+r3+r4 where the ri are the radii of four spheres with centers at the vertices and mutually tangent.
The tangent points of these spheres are also the tangent points of the edges with the mid-sphere; the intersections of the mid-sphere with the tetrahedron's faces are the incircles of the faces.
The three segments joining the tangent points on two opposite edges converge.
See also Soddy's "kissing spheres". |
|
nets of tetrahedra
| The net of the regular tetrahedron is well known (an equilateral triangle with its midpoint triangle); the net of the regular trirectangle tetrahedron can be easily deduced. |
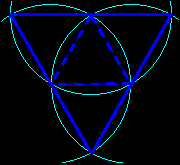 |
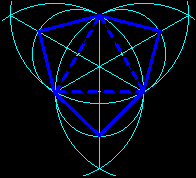 |
| Here is the second net of the regular tetrahedron: |
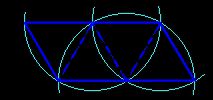 |
A triangle folded along the sides of its midpoints triangle is the net of an equifacial tetrahedron (the triangle must have three acute angles).
Three folds a square into the net of a tri-right-angled tetrahedron.
A square may also be the net of an equifacial tetrahedron.
| 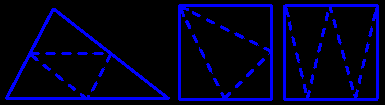 |
If we pull one lateral face of a pyramid down on the plane of its base, we notice that the altitude of this face swings around its foot. We deduce the construction of a net of a tetrahedron:
We choose the base triangle and a point S (projection of the summit) which may be chosen on a side or outside of the base triangle. Each lateral triangle has an altitude coming through S, on which lays its third vertex. We choose one of them (S' for example, with HS'>HS) and deduce the two others by transferring the lengths of the sides.
We may choose the height SS'=h of the tetrahedron by constructing the right-angled triangle HSS'. |
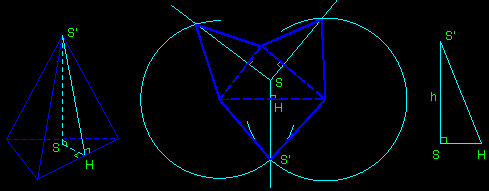 |
cuttings through a tetrahedron
| If we cut a tetrahedron SABC using a plane parallel to the face ABC, for example at mid-high, we get a pentahedron (truncated pyramid with three trapezoid lateral faces), whose volume is 7/8 of the tetrahedron's volume.
The altitudes of the three trapeziums are obviously not equal, but there is a direction in the space according to which they seem to be. We may search it experimentally by moving the solid. |
|
| Let's switch from the space to the plane by projecting the summit S to S' on the plane (ABC). The section at mid-high is then a triangle A'B'C', and the midpoint theorem in a triangle proves that A'B'C' is a reduction of ABC (for a reduction ratio different from 1/2 we use Thales theorem, or an homothecy with center S'). In order to have three trapeziums with same altitude, it is necessary and sufficient for each vertex of A'B'C' to be equidistant from two sides of ABC, thus laying on the bisector of the sector. Finally, S' has to be the incenter I of ABC. The searched direction is (SI). |
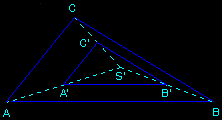 |
Here are three exercises (computations and constructions) to test your mastery of the space :
• Compute the volume of a regular tetrahedron with edge a, and the measure of the angle of two faces.
How to verify these results?
• Draw in perspective a tetrahedron SABC, and chose on its surface three points P, Q an R not on the same face. Construct the section of SABC by the plane (PQR).
The construction is easy if one point lays on an edge or if two points lay on a same face.
If not you have to tire yourself a little more to get the solution.
• Construct a tetrahedron with given volume knowing the directions and the lengths of two opposite edges.
| reference: |
Géométrie de l'espace et du plan (in French) by Yvonne and René Sortais (published by Hermann - 1988) pages 305-336 |
See also the pages devoted to the decompositions of the parallelepiped, to the tetrahedral symmetries and to the kaleidocycles.
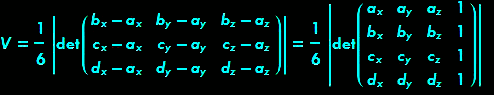




 projection
projection 





