miscellaneous animations of non convex polyhedra

with 12 star pentagons...

Here are two uniform polyhedra whose 60 edges are the diagonals of the 12 pentagonal faces of the regular dodecahedron and the icosidodecahedron.

small ditrigonal icosidodecahedron
20 self-intersecting equilateral triangles form 30 hollows.
dual: the first stellation of the icosahedron

dodecadodecahedron (2x12 pentagons)
12 self-intersecting convex pentagons form 20 cavities.
dual: a stellation of the rhombic triacontahedron

dodecahedra...

compound of two regular dodecahedra
(assemblages of "roofs" on the six faces of a cube)

dodecahedron augmented / excavated
with a pyramid on each face

"golden dodecahedron" by Jean Pedersen
(no symmetry plane, can be braided with six strips)

an "anti-parallelepiped"

This compound of two symmetric tetrahedra is a distorted anticube.


The figure may be dynamically modified
by moving the four yellow points with the mouse pointer.

two sequences of polyhedra

The polyhedra of this sequence have 4n faces which are all half squares. They have been discovered by a visitor, J.-P. Lhermet, following a mistake in the assemblage of an IsoAxis.
For n=3 we get... the cube.
The net is a "zigzag" of squares extracted from the IsoAxis grid.

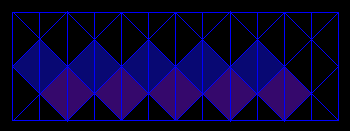net net for n=5, that is 20 faces
(it has to be folded alternatively in each way)


This sequence of "plexagons" has been described by Paul Bourke: the nets of these polyhedra are made of two identical hexagons. To build the polyhedron, pleat the hexagons as shown below, turn one up-down and rotate it by 60° and assemble the two pieces.

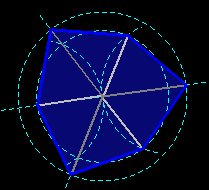
patron
The animation modifies the radius of the external circle in the drawing.

references: •  Build Your Own Polyhedra  by Hilton and J.Pedersen, Addison-Wesley Publishing Company, 1988 (pages 107-110, 123)
•  "Plexagon - Pleated Hexagon" web page by Paul Bourke

home page
French 		convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects January 2001
updated 15/12/2015