Pour n=3 on obtient... le cube.
Le patron est un "zigzag" de carrés extrait de la grille IsoAxis.
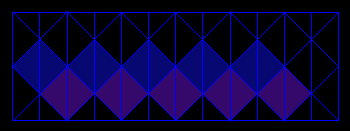patron pour n=5, soit 20 faces
(les plis se font alternativement dans chaque sens)
Cette suite de "plexagones" a été décrite par Paul Bourke : les patrons de ces polyèdres sont constitués de deux hexagones identiques. Pour construire le polyèdre, plissez les hexagones comme indiqué ci-dessous, retournez l'un et tournez-le de 60°, et assemblez les deux pièces.
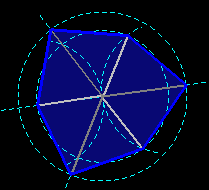
L'animation modifie le rayon du cercle extérieur sur le dessin.
