
D'autres positions remarquables et une animation de cet étonnant objet
sont présentées sur deux autres pages.

D'autres positions remarquables et une animation de cet étonnant objet
|
Si, après l'avoir allongée d'un nombre pair de bandes, on déforme la grille en rapprochant les bandes extrêmes, on obtient d'autres objets aussi étonnants dont la manipulation devient délicate. Les possibilités sont infinies.
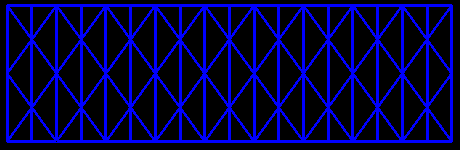 |
Cette grille de 18 bandes de triangles d'or (36°-108°-36°) conduit à un objet dont quatre vues sont présentées sur une autre page. |
Pour découvrir cette petite merveille, il vous faudra reproduire la grille et procéder au pliage et à l'assemblage en réunissant les bandes extrêmes (comme on le ferait pour créer un prisme droit régulier). La beauté se mérite ! IsoAxis vous récompensera largement de vos efforts. De plus, rien n'interdit de colorier ou de décorer les triangles pour augmenter le plaisir visuel.
Tous les patrons présentés sont destinés à être reproduits par constructions géométriques (règle et compas ou logiciel de dessin) ; ils sont accompagnés d'indications suffisantes pour ce faire. Je n'utilise pas de languettes de collage ; par expérience je préfère le ruban adhésif qui permet des assemblages plus précis et conduit à des objets plus robustes.

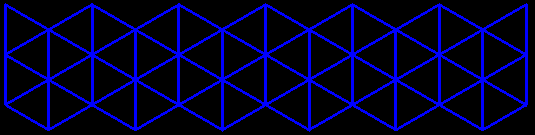
La chaîne de tétraèdres se referme sans problème si leur nombre est pair ; en effet les tétraèdres sont équifaciaux avec deux arêtes opposées orthogonales qui servent de liaisons entre eux. On peut donc créer une infinie variété de kaléïdocycles.
On a prouvé que le nombre de tétraèdres (non réguliers) peut être réduit à 6, et que "l'oeil" de l'anneau peut être réduit à un point quand les arêtes de liaison sont coplanaires.
Il existe aussi des kaléïdocycles où toutes les faces des tétraèdres sont des triangles rectangles ; le "cube de Schatz" est une telle configuration remarquable d'ordre 6.
Soyez patients pendant l'initialisation ! (rechargez la page si une animation ne démarre pas)
kaléïdocycle régulier d'ordre 12 |
kaléïdocycle fermé d'ordre 12 |
kaléïdocycle rectangle d'ordre 12 |
Si on utilise une grille oblique de triangles comme patron, on peut obtenir un kaléïdocycle torsadé ; la chaîne de tétraèdres se referme alors comme un ruban de Möbius. La description mathématique de ces objets était un beau défi relevé par Marcus Engel ; son animation paramétrée englobe différents types de kaléïdocycles, y compris les torsadés (dont le nombre de tétraèdres peut être impair).
| références : |
• Le remarquable SITE DE MARCUS ENGEL http://www.kaleidocycles.de/intro.shtml n'est plus accessible ; voici des copies de son travail sur la théorie des kaléïdocycles avec l'applet qui permet de visualiser tous les types de kaléïdocycles, et quelques patrons
• M.C.Escher kaléïdocycles par Doris Schattschneider et Wallace Walker (Taco - 1988), en anglais avec 17 patrons de polyèdres et de kaléïdocycles décorés par des "motifs périodiques" de M.C.Escher • Metamorphs par Robert Byrnes, en anglais (Tarquin Publications - 2004), avec 14 patrons d'objets que l'on peut tourner sur eux-mêmes (dont 7 kaléïdocycles) • kaleidocycles "bricolage mathématique" par Jürgen Köller (en anglais) • une étude élémentaire du kaléïdocycle fermé d'ordre 6 par Xavier Hubaut • Les kaléïdocycles irréguliers fermés par Carole Le Beller • A Group Theoretic Approach to Kaleidocycles and Cubeocycles par Lisa Marie Bush (en anglais) • des kaléïdocycles et autres modèles en papier - collection de Karine Lombard |
d'autres kaléïdocycles : kaléïdo 1 - kaléïdo 2 - AniKA (Marcus Engel)
page accueil
 |
polyèdres convexes - polyèdres non convexes - polyèdres intéressants - sujets connexes | février 2000 mis à jour 13-03-2009 |