Le "cube de Paul Schatz" contient un kaléïdocycle d'ordre 6 dont une position esquisse un cube que l'on peut compléter avec deux "coins" (symétrie d'ordre 3).
Pendant la rotation on note deux intéressantes "positions triangulaires".
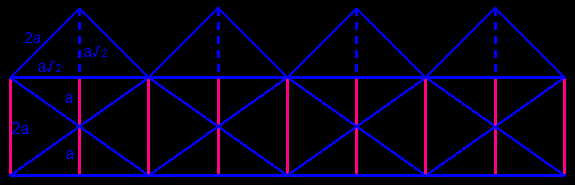
Le patron de ce kaléïdocycle est facile à dessiner : douze triangles sont des demi-rectangles (longueur double de la largeur) et les douze autres sont des demi-triangles équilatéraux.
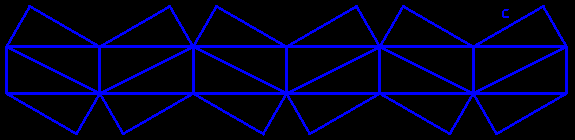
Le volume du kaléïdocycle est le tiers du volume du cube.
preuve : la base des six pyramides est un demi-triangle équilatéral dont le grand côté, double du petit, est le côté du triangle équilatéral, et le troisième en est la hauteur qui est égale à l'arête c du cube ; la hauteur de ces pyramides est égale au petit côté de leur base, soit (1/2)×c/(√3/2) = c√3/3 ; le volume du kaléïdocycle est donc 6×1/3×(1/2×c×c√3/3)×c√3/3 = c³/3.
Ce "cube" est lié à un curieux objet géométrique : l'oloïde, une autre découverte de Paul Schatz.
LiveGraphics3D a des difficultés à bien afficher toutes les faces