
six icosidodécaèdres tronqués emboîtés
résine epoxy - George W. Hart)

sept polyèdres de Goldberg emboîtés
(FDM - George W. Hart)

projection du 4D-120-tope
(George W. Hart)
Les ordinateurs, avec leur puissance de calcul et les performances des cartes graphiques, ont permis de rapides progrès de la recherche sur les polyèdres. Internet offre de multiples ressources tant sur les connaissances classiques que sur les résultats récents (par exemple l'utilisation du facettage). Les applets Java permettent de belles présentations interactives.
De nouveaux programmes performants, disponibles gratuitement ou à des prix modestes, permettent maintenant à chacun d'explorer le monde fascinant et infini des polyèdres. Parmi les plus remarquables, citons Hedron de Jim McNeill, Polyhedra Stellations de Vladimir Bulatov, et Great Stella ou Stella4D de Robert Webb.
Parmi les centaines de sites consacrés aux polyèdres, le plus vaste et le plus complet est Virtual Polyhedra de George W. Hart. A partir du "globe de liens" vous pouvez accéder à mes préférés.
Différentes définitions d'un polyèdre conduisent à différents objets mathématiques : solides ou surfaces ou ensembles de points (sommets ), ou de segments (côtés ) organisés en "polygones" (faces ).
Dans Are Your Polyhedra the Same as My Polyhedra? (en anglais), Branko Grünbaum utilise une définition générale qui permet de nouvelles classes de polyèdres où des points représentant des sommets distincts coïncident ; les arêtes peuvent donc être de longueur 0 ou colinéaires (se chevaucher ou coïncider). Il est intéressant de voir comment de nouveaux critères cohérents conduisent à de nouveaux "polyèdres réguliers".
Dans It's a long way to the stars or The sorry state of polyhedron theory today Guy Inchbald pointe du doigt plusieurs "bugs" dans la théorie des polyèdres.
Stellation et facettage sont deux procédures duales. Des études récentes sur la stellation de l'icosaèdre et le facettage du dodécaèdre montrent que les définitions actuelles manquent de précision quand on aborde les structures internes de ces polyèdres (les parties non visibles de l'extérieur). Par exemple la correspondance (dualité) entre stellations de l'icosaèdre et facettages du dodécaèdre pose souvent des problèmes que les notations habituelles ne permettent pas d'appréhender de façon satisfaisante.
Par ailleurs de nouvelles règles permettent d'ajouter quelques "icosaèdres perdus" (In search of the lost icosahedra de Guy Inchbald) à la fameuse liste des "59 icosaèdres" (The fifty nine icosahedra de Coxeter, Du Val, Flather et Petrie) établie il y a soixante ans.
| référence : | http://www.steelpillow.com/polyhedra/ |
"Rapid Prototyping" recouvre différentes techniques où un objet en 3D décrit par un fichier informatique est fabriqué par une machine qui calcule les sections et agglutine des centaines de très fines couches de matières. Très précis, les modèles ainsi réalisés restent de taille limitée et onéreux, mais les choses peuvent évoluer rapidement.
Ces nouvelles techniques d'impression en 3D (stéréolythographie, Deposition Modeling, Selective Laser Sintering) permettent de réaliser des objets géométriques compliqués (polyèdres emboîtés, projections de polytopes...) en évitant le fastidieux assemblage final. De nouvelles technologies continuent d'apparaître : PolyJet inkjet technology, 3 Dimensional Printing, Electron Beam Melting... Les prix des imprimantes 3D baissent rapidement et deviennent accessibles au grand public.
Des fichiers de description et des services d'impression 3D sont évidemment disponibles sur internet.

six icosidodécaèdres tronqués emboîtés résine epoxy - George W. Hart) |

sept polyèdres de Goldberg emboîtés (FDM - George W. Hart) |

projection du 4D-120-tope (George W. Hart) |

6 cubes entrelacés (SLS, nylon - Rinus Roelofs) |

icosidodécaèdre en 6 anneaux (SLS, nylon - Rinus Roelofs) |
sculpture originale d'Escher (1940)
En 2000 Jane Yen et Carlo Séquin ont développé un système interactif pour concevoir des sphères d'Escher - balles sphériques composées de tuiles identiques. Le programme crée des pavages sphériques en utilisant les groupes polyédriques de rotations. Vous pouvez choisir un groupe d'isométries et dessiner votre propre tuile avec un bas-relief... même si vous ne disposez pas de machine FDM pour "imprimer" votre travail. Une jolie sphère d'Escher apparaît quand les tuiles sont assemblées sur une balle de tennis. |
 |
 |
 |
 |
 |
Rappel : en 4D, le "120" - équivalent du dodécaèdre régulier en 3D - est limité par 120 cellules (dodécaèdres réguliers), quatre par sommet, trois par arête et deux par face. Le puzzle est composé de 1+12+20+12=45 dodécaèdres imprimés en 3D : seul le premier - au centre - est régulier, les autres sont plus ou moins aplatis (déformations dues à la projection de 4D sur un 3D-hyperplan) et disposés en trois couches successives. Les projections des 30 cellules orthogonales à l'hyperplan de projection sont les faces hexagonales (dodécaèdres aplatis) du dodécaèdre chanfreiné qui contient l'assemblage des 45 pièces. Les projections des 120-45-30=45 cellules restantes sont les mêmes 45 dodécaèdres (voir aussi une animation de ce puzzle). |
 |
| références : | http://www.georgehart.com/rp/rp.html
Escher sphere construction kit : article illustré (en anglais) - le site web avec d'autres photos n'existe plus (programme à télécharger) symmetry, un PowerPoint (4,3 Mo) par George Hart : groupes, sculptures (M.C. Escher), impression en 3D (sphères par Carlo Séquin) Le 120 (hyperdodécaèdre) de Arnaud Chéritat - Images des Mathématiques, CNRS, 2012 |
L'étude des assemblages de polyèdres par des arêtes de liaison servant de charnières n'est pas nouvelle ; les plus connus de ces solides "mobiles" sont sans doute les kaléïdocycles (anneaux de tétraèdres que l'on peut tourner sur eux-mêmes).
C'est assez récemment, avec Paul Schatz (1898-1979), que débute la recherche systématique de solides platoniciens éversibles. Il existe des publications concernant ces objets, mais essentiellement en allemand. Il n'existe donc pas de vocabulaire standard pour désigner cette notion : Umstülpen peut se traduire par "retourner".
éversibilité : quand l'intérieur d'un solide peut être retourné vers l'extérieur, ou l'extérieur vers l'intérieur.
En plus de l'espace, tous les éléments géométriques d'un polyèdre régulier peuvent être "inversés" en même temps. Les polyèdres sont séparés en au moins trois pièces, dont au moins un kaléïdocycle, qui permettent de retourner le polyèdre "de l'intérieur vers l'extérieur" : ils sont décomposés en pyramides avec un sommet commun au centre et réassemblés en "stellations" avec une cavité identique au polyèdre original. De belles et intéressantes positions intermédiaires apparaissent au cours de la transformation ; les formes positives (départ) et négatives (arrivée) ont même groupe de symétrie. On pouvait acquérir un ensemble de sept remarquables modèles de ces polyèdres platoniciens éversibles mais ils ne semblent plus disponibles.
|
|
|
Voici un anneau en zigzag de 12 tétraèdres qui se plie en un cube dont les arêtes sont les arêtes de liaison mais qui n'est PAS un kaléïdocycle (sur chaque tétraèdre les arêtes de liaison sont perpendiculaires, donc adjacentes et non opposées comme pour les kaléïdocycles). Ce curieux objet, également conçu par Naoki Yoshimoto, permet d'obtenir, entre autres, d'intéressantes configurations triangulaires. Ce "flexaèdre" est un CUBE ÉVERSIBLE : il peut être retourné pour former un dodécaèdre rhombique avec une cavité cubique limitée par les faces retournées du cube original.
Voici un extrait d'une vidéo (3'24 - 12 Mb) de Mickaël Launay (Micmaths) trouvée sur YouTube (environ 7 minutes).
|
|
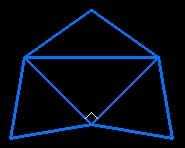
le patron d'un tétraèdre est un demi-carré (a-a-a√2) entouré par trois triangles isocèles avec deux côtés de longueur a√3/2 |
|
Différents modèles du type puzzle, plus ou moins apparentés à Umstülpung sont disponibles sur internet (voir liens ci-dessous). Ils sont tous intéressants et parfois complexes et difficiles à remettre dans leur configuration originale quand on a fini de jouer avec !
| références : |
• Umstülpkörper par Ellen Pawlowski (2005, en allemand)
• Umstülpung - konkret und virtuell par Ellen Kneppeck-Pawlowski (2008, en allemand) et son site internet consacré aux "solides éversibles" (Umstülpkörper en allemand) • Umstülpung - Geometrische Raumstrukturen par Margarita Ehrlich (2005, en allemand) • Development of mathematical imagination of 3-dimensional polyhedra throughout history and inversion phenomena par Alexander Heinz (en anglais) • eversible polyhedra models critique par Gerald L. Alexanderson et Jean Pedersen (en anglais) • vidéos : flyping-games - boutiques en ligne : en allemand, en anglais |
page accueil
 |
polyèdres convexes - polyèdres non convexes - polyèdres intéressants - sujets connexes | février 2004 mis à jour 22/04/2024 |