
six nested truncated icosidodecahedron
(epoxy resin - George W. Hart)

seven nested Goldberg polyhedra
(FDM - George W. Hart)

projection of the 4D-120-cell
(George W. Hart)
Computers,with their calculation power and the performance of their graphic cards, have allowed rapid progresses in research about polyhedra. The Internet offers numerous resources on classical knowledge as well as on recent results (for example the use of faceting). Java applets allow nice interactive presentations.
New high-performance programs, available for free on at a modest price, give now every one the opportunity to explore the fascinating and infinite polyhedra's world. Among the most outstanding let's held up Hedron by Jim McNeill, Polyhedra Stellations by Vladimir Bulatov, and Great Stella or Stella4D by Robert Webb.
Among the hundreds of sites devoted to polyhedra the vastest and most complete is Virtual Polyhedra by George W. Hart. From the "link's globe" you may access to my favorites.
Different definitions of a polyhedron lead to different mathematical objects: solids ou surfaces or sets of points (vertices ), or of line-segments (edges ) organized in "polygons" (faces ).
In Are Your Polyhedra the Same as My Polyhedra? Branko Grünbaum uses a general definition which allows new classes of polyhedra where points representing distinct vertices coincide; edges may thus be of length 0 or collinear (overlapping or coinciding). It's interesting to see how new consistent criteria lead to new "regular polyhedra".
In It's a long way to the stars or The sorry state of polyhedron theory today Guy Inchbald points out several "bugs" in the polyhedron theory.
Stellation and faceting are two dual procedures. Recent studies on the stellation of the icosahedron and faceting of the dodecahedron show that the current definitions are lacking precision when the internal structures (the parts non visible from the exterior) of these polyhedra are involved. For example the correspondence (duality) between stellations of the icosahedron and facetings of the dodecahedron leads to problems which cannot be well managed with the current notations.
Furthermore new rules allow to add a few "lost icosahedra" (In search of the lost icosahedra by Guy Inchbald) to the famous list of "59 icosahedra" (The fifty-nine icosahedra by Coxeter, Du Val, Flather and Petrie) established sixty years ago.
| reference: | http://www.steelpillow.com/polyhedra/ |
"Rapid Prototyping" covers different techniques where a 3D object described by a computer file is fabricated by a machine which calculates the cross sections and sticks together hundreds of very thin layers of material. Very accurate, the RP models remain limited in size and expensive, but things may quickly evolve.
These new 3D-printing techniques (stereolithography, Fused Deposition Modelling, Selective Laser Sintering) allow to carry out complex geometric objects (nested polyhedra, projections of polytopes) without the need of tedious final assemblage. New technologies continue to appear: PolyJet inkjet technology, 3 Dimensional Printing, Electron Beam Melting...
Description files and online 3D printing services are obviously available on the internet.

six nested truncated icosidodecahedron (epoxy resin - George W. Hart) |

seven nested Goldberg polyhedra (FDM - George W. Hart) |

projection of the 4D-120-cell (George W. Hart) |

6 interlaced cubes (SLS, nylon - Rinus Roelofs) |

6-rings icosidodecahedron (SLS, nylon - Rinus Roelofs) |
original sculpture by Escher (1940)
In 2000 Jane Yen and Carlo Séquin developed an interactive system to design Escher Spheres - spherical balls composed of identical tiles. Using the polyhedral rotational groups the program creates spherical tessellations. You can chose a group of symmetries and draw your own tile with a bas-relief... even if you don't have a FDM machine to "print" your work. A nice Escher sphere appears when the tiles are assembled on a tennis ball. |
 |
 |
 |
 |
 |
Reminder: in 4D, the "120-cell" - equivalent of the regular dodecahedron in 3D - is limited by 120 cells (regular dodecahedra), four per vertex, three per edge and two per face. The puzzle consists of 1+12+20+12=45 dodecahedra printed in 3D: only the first - at the center - is regular, the others are more or less flattened (distortions due to the projection from 4D on a 3D-hyperplane) and laid-out in three successive layers. The projections of the 30 cells orthogonal to the projection's hyperplane are the hexagonal faces (flattened dodecahedra) of the chamfered dodecahedron which contains the assembling of the 45 pieces. The projections of the 120-45-30=45 remaining cells are the same 45 dodecahedra (see also an animation of this puzzle). |
 |
| references: | http://www.georgehart.com/rp/rp.html
Escher sphere construction kit: illustrated paper (PDF, 1.1 Mb) - the web site with more photos disappeared (program to download) symmetry, a PowerPoint show (PPS, 4.3 Mb) by George Hart: groups, sculptures (M.C. Escher), 3D printing (spheres by Carlo Sequin) Le 120 (120-cell or hyperdodecahedron) by Arnaud Chéritat - Images des Mathématiques, CNRS, 2012 (in French) |
The study of polyhedra assemblings using link edges as hinges isn't new; the best known of these "mobile" solids are no doubt the kaleidocycles (rings of tetrahedra which can be turned around themselves).
The systematic research of eversible platonic solids began quite recently with Paul Schatz (1898-1979). There are publications about these objects, but mostly in German. Thus there is no standard vocabulary to describe this notion: Umstülpen may be translated by "turn inside outside".
eversibility: when the interior of a solid can be turned outwards or the outside inwards.
Not only the space, but also all the geometric elements of a regular polyhedron can be "inverted" at the same time. The polyhedra are broken into at least three pieces, among then at least one kaleidocycle, which allow to turn the polyhedron "inside outside": the are dissected into pyramids with a common vertex at the center and reassembled into "stellations" with a hole identical to the original polyhedron. Interesting intermediate positions appear during the transformation; the positive (start) and negative (arrival) forms have same symmetry group. It was possible to buy a set of seven outstanding models of these platonic eversible polyhedra, but they seem no longer available.
|
|
|
Here is a zigzag ring of 12 tetrahedra which fold as un cube whose edges are the link edges, but it is NOT a kaleidocycle (on each tetrahedron the link edges are perpendicular, thus adjacent and not opposite as for kaleidocycles). This curious objet, also designed by Naoki Yoshimoto, allows, among others, interesting triangular configurations. This "flexahedron" is an eversible cube: it may be turned inside outside to build a rhombic dodecahedron with a cubic hole limited by the turned over faces of the original cube.
Here is an excerpt of a video (3'24 - 12 Mb) by Mickaël Launay (Micmaths) found on YouTube (about 7 minutes, in French).
|
|
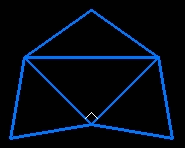
the net of the tetrahedron is a half square (a-a-a√2) surrounded by three isosceles triangle with two sides of length a√3/2 |
|
Different puzzle models, more or less related to Umstülpung are available on the internet (see links below). All are interesting and sometimes complex and difficult to put back in their original configuration when you have finished to play with!
| references: |
• Umstülpkörper by Ellen Pawlowski (2005, in German)
• Umstülpung - konkret und virtuell by Ellen Kneppeck-Pawlowski (2008, in German) and her internet site devoted to the eversible polyhedra (Umstülpkörper in German) • Umstülpung - Geometrische Raumstrukturen by Margarita Ehrlich (2005, in German) • Development of mathematical imagination of 3-dimensional polyhedra throughout history and inversion phenomena by Alexander Heinz • eversible polyhedra models revue by Gerald L. Alexanderson and Jean Pedersen • videos: flyping-games - online shops: in German, in English |
home page
 |
convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects | February 2004 updated 22/04/2024 |