other kaleidocycles   1/2

For the regular kaleidocycles the order minimum is 8; nevertheless we can build a ring with 6 tetrahedra, but which cannot turn completely.

kaleidocycles of minima orders

regular kaleidocycle of order 8

closed kaleidocycle (non regular) of order 6 may be cut using its symmetry plane (when closed) into two mirror image right-angled kaleidocycle

right-angled kaleidocycle of order 6 ("Schatz cube" below)


The "Paul Schatz cube" contains a kaleidocycle of order 6 one position of which sketches a cube which may be completed with two "bolts" (order 3 symmetry).
During the rotation we notice two interesting "triangular positions".
 
 
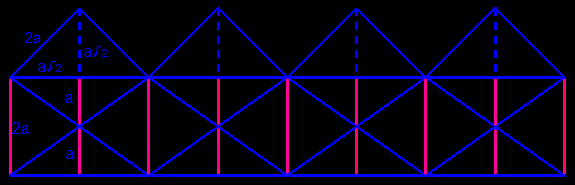
The net of this kaleidocycle is easy to draw: the twelve triangles which build the rectangle have one side of their right angle with a length double of that of the other side, and the twelve others are half equilateral triangles.

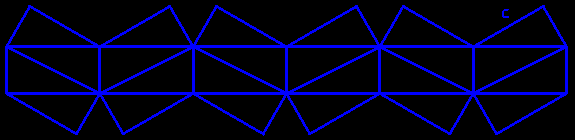
net (Schatz ring)
The volume of the kaleidocycle is one third of the volume of the cube.
proof: the base of the six pyramids is a half equilateral triangle whose long side, twice the small side, is the side of the equilateral triangle, and the third is its height which is equal to the edge c of the cube; the height of these pyramids is equal to the short side of their base base, i.e. (1/2)×c/(√3/2) = c√3/3; the volume of the kaleidocycle is therefore  6×1/3×(1/2×c×c√3/3)×c√3/3 = c³/3.

This "cube" is linked to a curious geometric object: the oloid, another discovery by Paul Schatz.


LiveGraphics3D has difficulties to display well all the faces


The "Konrad Schneider cube" contains a kaleidocycle of order 8 one position of which also sketches a cube which may be completed with two "bolts" (order 4 symmetry).
During the rotation we notice interesting "square positions".
The three pieces build the eversible cube (Umstülpwürfel  in German) : we move from the cube (positive form) to the rhombic dodecahedron (negative form) with a cavity equal to the initial cube.
 
 
The net of the kaleidocycle is easy to draw starting with a strip of eight format A (a√2×2a) rectangles. net (Schneider ring)
The eight link edges (four of length a and four of length 2a) are drawn in magenta (the pairs of the small ones superimpose themselves). The dashed segments point out cuts.


references: •  the site by Jürgen Köller (special kaleidocycles, also in German)
•  Umstülpkörper  by Ellen Pawlowski (2005, in German)
•  see also  eversible  polyhedra

more kaleidocycles: IsoAxis - kaleido 2 - AniKA (Marcus Engel)

home page
French 		convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects February 2000
updated 16-03-2024