other kaleidocycles   2/2

right-angled kaleidocycle of order 8

kaleidocycle of order 10

kaleidocycle of order 16



This "Yoshimoto cube" is built with 24 identical pyramids assembled in two kaleidocycles of order 12.
The net of one of these kaleidocycles is easy to draw: each vertical strip is the net of a tetrahedron, the twelve vertical rectangles are of format A, and the triangles above are isosceles right angled (half square).

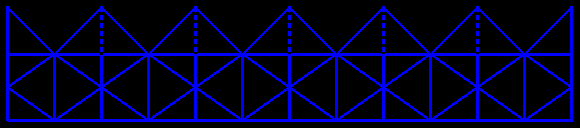net (half Yoshimoto cube)


On the left, one of the tetrahedra in a "half cube". Its faces are:
 •  an isosceles right angled triangle (a quarter of a face of the cube),
 •  two right angled triangles (two halfs of a format A rectangle),
 •  an isosceles triangle, union of two of these right angled triangles.
 
On the right, one of the kaleidocycles folded in a "half cube"; the magenta lines show the 12 hinges: the six largest are edges of the cube, the six smallest join the center of the cube to the centers of five faces (the red line shows two superimposed hinges).


 variant    By grouping the tetrahedra together by pairs and using the cube's edges as link edges we get ONE zigzag ring of 12 tetrahedra which is NOT a kaleidocycle (on each tetrahedron the link edges are perpendicular, thus adjacent and not opposite as for kaleidocycles). This curious objet, also designed by Naoki Yoshimoto, allows, among others, interesting triangular configurations. This "flexahedron" is an "eversible" cube: it may be turned inside outside to build a rhombic dodecahedron with a cubic hole limited by the turned over faces of the original cube.
Here is an extract of a video (3'25 - 12 Mb) by Mickaël Launay (Micmaths) found on YouTube (about 7 minutes, in French).

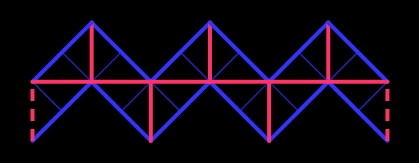net (flexahedron)
one of the tetrahedra in a cube lay out the twelve tetrahedrons on their rectangular faces as indicated above
it remains to assemble them according to the eleven hinges (in magenta); the twelfth (in dotted lines) will close the ring
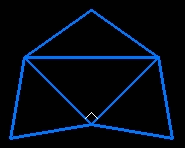
net (tetrahedron)

the net consists of a half square (a-a-a√2) surrounded by three isosceles triangle with two sides of length a√3/2 the ring folded in the cube whose edges are the 12 hinges (in magenta); the have three by three a common end, except on the ends of a diagonal where the three ends are superimposed but free, so the cube can open itself along that diagonal

references: •  the Shinsei Miracle (in German)
    and other assemblings of kaleidocycles: tetra one - cube one
•  online shops: Kuboid GmbH - flyping-games

more kaleidocycles: IsoAxis - kaleido 1 - AniKA (Marcus Engel)

home page
French 		convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects February 2000
updated 16-08-2016