Ce "cube de Yoshimoto", aussi connu sous le nom de "Shinsei Miracle", est constitué de 24 pyramides identiques assemblées en deux kaléïdocycles d'ordre 12.
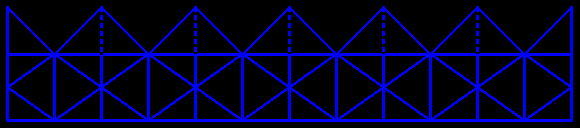
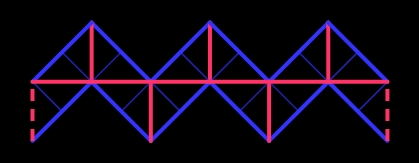
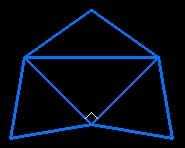
Le patron de ces kaléïdocycles est facile à dessiner : chaque bande verticale est le patron d'un tétraèdre, les douze rectangles verticaux sont de format A, et les triangles du haut sont rectangles isocèles (demi carré).