
Other outstanding positions and an animation of this amazing object
are presented on two other pages.

Other outstanding positions and an animation of this amazing object |
If we extend it using an even number of strips, and then distort the grid by bringing the extreme strips closer, we get other astonishing forms which handling becomes tricky. The possibilities are infinite.
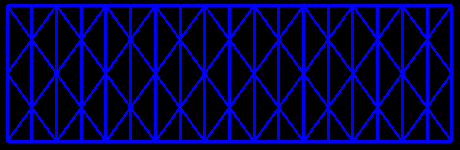 |
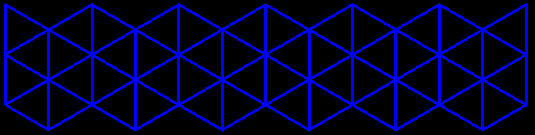
This grid of 18 strips of golden triangles (36°-108°-36°) leads to a similar object ; four views of it are presented on an other page. |
To discover this little wonder, you will have to reproduce the grid, fold it and assemble the extremes (as you would do to create a regular right prism). The beauty has to be deserved! IsoAxis will greatly reward your efforts. You may color or decorate the triangles to increase the visual pleasure.
All the nets presented are intended to be reproduced by geometric constructions (ruler and compasses or drawing software); they come with sufficient indications to do so. I don't use tabs to be glued; by experience I prefer adhesive tape which allows more precise assemblings and leads to more robust objects.

The ring of tetrahedra closes up without problem if their number is even; actually the tetrahedra are equifacial with two opposite orthogonal edges which are used as links between them. So we can create an infinite variety of kaleidocycles.
It has been proved that the number of (non regular) tetrahedra can be reduced to 6, and that the "eye" of the ring can be reduced to a point when the link edges are coplanar.
There are also kaleidocycles where all the faces of the tetrahedra are right triangles; the Schatz cube is an outstanding such configuration of order 6.
Be patient during the initialization! (reload the page if an animation doesn't start)
regular kaleidocycle of order 12 |
closed kaleidocycle of order 12 |
right-angled kaleidocycle of order 12 |
If we use an oblique grid of triangles as pattern, we may get a twisted kaleidocycle; the chain of tetrahedra looks then like a Möbius ribbon. Describing it mathematically was nice challenge taken up by Marcus Engel; his parametrized animation embraces different types of kaleidocycles, included the twisted ones (whose number of tetrahedra can be odd).
| references: |
• The outstanding SITE BY MARCUS ENGLE (http://www.kaleidocycles.de/intro.shtml) is no longer accessible; here are copies of his work about the theory of kaleidocycles with the applet which allows to visualize all types of kaleidocycles, and a few nets
• M.C.Escher kaleidocycles by Doris Schattschneider and Wallace Walker (Tarquin Publications - 1978) with 17 models of polyhedra and kaleidocycles decorated with "repeating patterns" of M.C.Escher • Metamorphs by Robert Byrnes (Tarquin Publications - 2004) with 14 models of objects which can be rotated on themselves (among them 7 kaleidocycles) • kaleidocycles "math DIY" by Jürgen Köller • to see: the nice kaleidocycles by Nicolas Hannachi ("Math à mâter "). • an elementary study of the closed kaleidocycle of order 6 by Xavier Hubaut (in French) • Les kaléïdocycles irréguliers fermés by Carole Le Beller (in French) • A Group Theoretic Approach to Kaleidocycles and Cubeocycles by Lisa Marie Bush • kaleidocycles and other paper models - collection of Karine Lombard |
more kaleidocycles: kaleido 1 - kaleido 2 - AniKA (Marcus Engel)
home page
 |
convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects | February 2000 updated 13-03-2009 |