Ce travail prétend générer l'animation par ordinateur d'un IsoAxis (décrit dans le paragraphe suivant) comme exemple d'une animation cinématique d'un système mécanique avec de multiples liaisons entre les éléments qui le composent, et avec divers degrés de liberté.
L'IsoAxis (patente USA n° 3302321) a été décrit par Wallace Walker en 1958, en travaillant sur un projet dont l'objectif était de trouver des structures à découper.
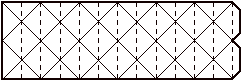
C'est un papier quadrillé plié en soixante triangles rectangles isocèles, formant un anneau tridimensionnel qui peut tourner sur lui-même en donnant un cycle de configurations d'apparence curieuse.
 |
 |
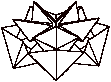
| Figure 1 : Développement et perspective d'un IsoAxis | |
Comme on peut le voir sur la figure 1, le système est formé par six secteurs de dix triangles chacun, disposés en intervalles de 60° pour former une structure annulaire.
[Cette présentation suppose une symétrie qui pas nécessairement réalisée dans la réalité ; cependant le mouvement normal de l'IsoAxis est symétrique, et, par ailleurs, le problème est suffisamment complexe en lui-même avec un sixième de l'anneau.]
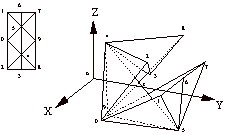
Pour obtenir la description cinématique de l'IsoAxis il est nécessaire de commencer par déterminer le nombre de degrés de liberté. Pour cela considérons un sommet quelconque du secteur présenté sur la figure 2, par exemple le 0. La position de ce point dans l'espace est fixée par trois coordonnées ; à partir de ce point on peut déterminer la position d'un autre point voisin (le point 5) moyennant deux coordonnées supplémentaires (par exemple deux coordonnées angulaires). Les deux points ainsi définis déterminent une droite ; l'ajout d'une autre coordonnée permet d'obtenir la position du troisième sommet du triangle (point 1). En raisonnant de même pour les points 1 à 6 (les points 7, 8 et 9 s'obtiennent par symétrie), on arrive à la conclusion que dix coordonnées sont nécessaires pour définir les positions de tous les points.
 |
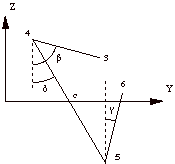 |
| Figure 2 : Secteur d'IsoAxis | Figure 3 : Définition des coordonnées angulaires
alpha = 1/2 <9c0> |
Maintenant si on ajoute les restrictions nécessaires pour que le secteur puisse faire partie d'un anneau (les points 0, 1 et 2 doivent se trouver dans le plan x=sqrt(3).y où sqrt(n) désigne "racine de n" ; les points 3 à 6 doivent se trouver dans le plan x=0), on obtient sept équations, ce qui fait descendre le nombre de degrés de liberté à trois. En fixant l'altitude du secteur, i.e. une coordonnée selon l'axe (Oz), on arrive finalement à deux degrés de liberté (sur la figure 3, le milieu du segment [45] est situé sur l'axe (Oy)).
Après avoir défini les angles alpha (a), béta (b), gamma (g) et delta (d) comme le montre la figure 3, on peut prendre delta et alpha comme degrés de liberté, de façon à ce que la rotation de l'IsoAxis soit directement associée à la variable delta.
Ainsi les coordonnées des points 0 à 6 seront données par :
Ces variables peuvent être calculées sous forme analytique en utilisant les équations traduisant les conditions d'orthogonalité entre segments et de distances entre points.
Note : on utilisera [nm] pour désigner le segment d'extrémités n et m, et |[nm]| pour désigner longueur de ce segment.
On commence par calculer le point 1 en utilisant les équations suivantes :
i. [05].[15] = 0
ii. |[15]| = sqrt(2)
qui s'écrivent :
iii. y1 ( x0/sqrt(3) + y0 - y5 ) + z1 ( z0 - z5 ) = y5 ( y0 - y5 ) + z5 ( z0 - z5 )
iv. (y1/sqrt(3) )2 + ( y1 - y5 )2 + ( z1 - z5 )2 = 2
Ce système admet deux solutions en (y1, z1) ; on prendra celle qui minimise l'angle <c51>.
Pour le cas z0=z5 :
y1 = ( y5 ( y0 - y5 ) ) / ( x0/sqr(3) + y0 -y5 )
x1 = y1/sqrt(3)
z1 = z5 +- sqrt( 2 - x12 - ( y1 - y5 )2 )
Sinon le système peut s'écrire sous la forme :
v. a y1 + z1 = b
vi. ( y1 sqrt(3) )2 + ( y1 - u )2 + ( z1 - v )2 = 2
avec
a = ( x0/sqrt(3) + y0 - y5 ) / ( z0 - z5 )
u = y5
b = z5 + y5 ( y0 - y5 )/( z0 - z5 )
v = z5
Il est donc possible d'obtenir y1 en fonction de (a,b,u,v), et on en déduit :
z1 = b - a y1
x1 = y1/sqrt(3)
Avec les coordonnées du point 1, il est possible de calculer la position du point 6, en utilisant la condition d'orthogonalité :
vii. [16].[56] = 0
d'où l'on tire :
viii. 1 = ( y1 - y5 ).sin(g) - ( z5 - z1 ).cos(g)
y6 = y5 + sin(g)
z6 = z5 + cos(g)
Il existe deux solutions en gamma ; on prend celle qui minimise l'angle <456>
Le calcul du point 2 est analogue à celui du point 1, en substituant le point 5 au point 4.
Le calcul du point 3 est analogue à celui du point 6 :
ix. 1 = ( y2 - y4 ).sin(b) - ( z2 - z4 ).cos(b)
De cette manière on peut déterminer les positions de tous les points en fonction de delta et de alpha.
Pour le moment on a calculé les coordonnées des points sans tenir compte d'une série de restrictions qui limitent les valeurs valides du paramètre alpha pour chaque valeur de delta. Ces restrictions proviennent d'une part de l'impénétrabilité des faces du secteur, et d'autre part de la nécessité de l'existence de solutions aux équations établies dans la partie précédente.
[Note : Comme on peut le constater sur les restrictions représentées, il existe une zone pour des valeurs de delta voisines de 90° où les courbes y5=0 et y4=0 tendent à délimiter une solution unique pour alpha. En pratique la solution s'avère non valide pour une des restrictions non analytiques ; ceci paraît signifier que le mouvement idéal, sans déformation du système, n'est pas possible.]
Quelques-unes de ces restrictions peuvent être posées et résolues facilement sous forme analytique, alors que d'autres peuvent seulement être résolues numériquement.
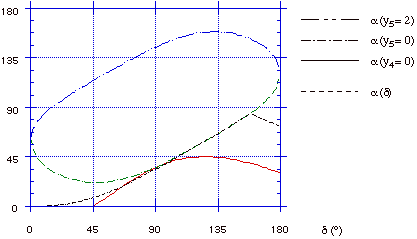
Pour y4 >= 0 l'équation est de la forme : 1 = A.sin(a) - B.cos(a)
avec A = sqrt(3) / sin(a) et B = -cos(d) / sin(d)
Ainsi la solution est directe.
La solution pour y5 >= 0 est analogue ; alors que pour y5 <= 2 la forme est la même,
avec A = sqrt(3) / ( 2 - sin(d) ) et B = -cos(d) / ( 2 - sin(d) )
Avec ces équations on peut délimiter le domaine de variation de alpha à une zone relativement étroite (les valeurs correspondant à la zone supérieure de la solution de y <= 2 peuvent conduire à des configurations valides, mais sans continuité avec celles qui forment le mouvement normal de l'IsoAxis).
La solution analytique des restrictions correspondant à l'existence de solutions pour les équations du second degrés doit se faire de façon numérique.
Les principaux problèmes qui apparaissent sont l'étroite marge de variation pour alpha dans quelques zones, et l'apparition de vibrations nettement perceptibles de quelques variables comme conséquence de variations minimes de l'angle alpha.
De fait, dans la zone correspondant à des valeurs de delta proches de 90°, on peut seulement obtenir une solution valide pour l'angle gamma si on autorise la coordonnée y4 à prendre des valeurs légèrement négatives (ce qui équivaut à admettre des déformations du modèle "réel"). La figure 5 permet de constater l'évolution de quelques variables significatives du modèle en fonction de delta. Les valeurs de gamma1 et gamma2 correspondent aux valeurs de l'angle <456>, exprimé en radians, pour les deux solutions possibles pour gamma.
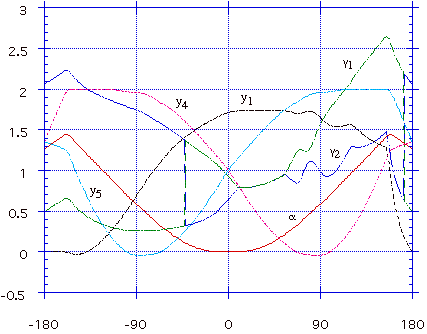
Notons que les variables y5 et y4, ainsi que y1, prennent des valeurs légèrement négatives en certains points ; ces valeurs doivent être positives, donc la seule solution consiste à admettre des déformations de la structure.
Pour la visualisation du modèle on a réalisé trois programmes entre 1991 et 1994 : l'un d'eux en utilisant l'interface RenderMan qui a permis d'effectuer une interprétation sur une machine quelconque, un autre utilise les fonctions de la librairie Starbase de HP, et un dernier, la librairie graphique GL de Silicon Graphics. Cela a permis de réaliser une animation en temps réel sur certaines machines conçues spécifiquement pour les calculs en 3D.
L'animation originale a été réalisée en 1993, en utilisant la version RenderMan sous Mac-OS.

Le code source de la version pour IRIS GL est disponible à http://phoebe.cps.unizar.es/~spd/src/graphics/isoaxis/
Il fonctionne en IRIS, mais ne devrait pas être trop difficile à adapter à Open GL multi-plateforme.
Note : Le code a été écrit il y a de nombreuses années, et aujourd'hui il serait bien plus clair. Peut-être le réécrirai-je pour Open GL...
Deux liens vers le site de Maurice Starck : "une balade dans le monde des polyèdres" :
http://www.polyhedra-world.nc/index.htm
http://www.polyhedra-world.nc/IsoAxis.htm
J.A. Gutierrez spd@daphne.cps.unizar.es (traduit en français par Maurice Starck - décembre 2003)
http://persephone.cps.unizar.es/%7Espd/isoaxis/