in a regular tetrahedron

Let's start by drawing a regular tetrahedron in perspective, and let's examine it to identify the elements whose measures we'll have to compute. regular tetrahedron
For symmetry reasons the orthogonal projection H of S on the plane (ABC) is the center of the equilateral triangle ABC; it lays thus at the two thirds of the median AK, that is AH=(2/3)AK and KH=AK/3
A good way to proceed consists of coming down in a plane by carrying out a pertinent cut through the polyhedron. Here the plane (ASH) is obvious: it contains the hight SH of the pyramid and the sides KA and KS of the angle of two faces.
Before starting the computation let's remember that
  •   the hight of an equilateral triangle with side a is a×√3/2, thus with BC=a, KA=KS=a×√3/2,
  •   the volume of a pyramid is the third of the product of the base's area by the altitude.
Hight SH (Pythagoras theorem in triangle ASH rectangular in H):  SH²=SA²-AH²= a²-[(2/3)×a×√3/2]² = (1-1/3)×a² = (2/3)×a²= h²  that is  h=(√2/√3)×a
Area of ABC:  (1/2)×BC×AK = (1/2)×a×(a×√3/2) = (√3/4)×a²
Tetrahedron's volume:  (1/3)×[(√3/4)×a²]×[(√2/√3)×a] = (√2/12)×a³
Angle of two faces:  cosθ = KH/KS = (a√3/6)/(a√3/2) = 1/3   thus   θ ≈ 70,53° ≈ 70°32'

These results are neither obvious, nor known by heart (except by a few genius!); it is thus suitable to verify them.

We can compute the volume again by using the cube in which the tetrahedron is naturally inscribed.
The diagonal of a face is equal to a (edge of the tetrahedron), thus the edge of the cube is c=a/√2.
To get the tetrahedron we have to cut off four "corners" of the cube (tri-rectangular tetrahedra with equilateral base). If we use one of the isosceles-rectangular face as base, the hight of a "corner" is c, and its volume   (1/3)×(c²/2)×c = c³/6
we deduce the tetrahedron's volume: c³-4(c³/6) = c³/3 = (a/√2)³/3 = (√2/12)×a³
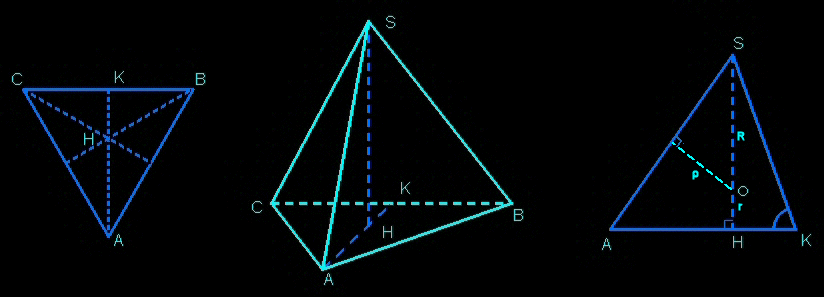
Corollary 1: the hight of the tri-rectangular tetrahedron relative to the equilateral face is the third of the cube's diagonal (d=c√3).
From   V = (1/3)×A×h   we deduce   h = 3V/A = 3[c³/6]/[(1/2)×(c√2)×(c√2)(√3/2)] = c/√3 = c√3/3 = d/3
Corollary 2: The circumsphere (defined by the four vertices) is, by symmetry, centered at the intersection point of the altitudes; its center O lays at the quarter of each altitude (starting from the base), its radius is thus  R = (3/4)×h.
proofs: •  O is the isobarycentre of the vertices  O = bar[A(1),B(1),C(1),S(1)] = bar[bar[A(1),B(1),C(1)],S(1)] = bar[H(3),S(1)]  situated at the quarter of HS
            •  One may also use the cube which has four vertices which define the tetrahedron; the two polyhedra have same circumsphere.
An altitude of the tetrahedron lays on a diagonal of the cube and  h=(2/3)d  thus  R = d/2 = 1/2×(3/2)h = (3/4)×h
verification: a=c√2, d=c√3 and h=(2/3)d  lead to  R = d/2 = (3h/2)/2 = (3/4)×h  or  R = (c√3)/2 = ((a/√2)√3)/2 = a×(√6/4) = a(√2/√3)×(3/4) = h×(3/4)
remarks: radius of the insphere (tangent to the faces, center O) : r = h/4 = R/3 = a×(√6/12)
               radius of the midsphere (tangent to the edges, center O): by Pythagoras theorem  ρ² = R²-(a/2)² which gives  ρ = a(√2/4)

Since we don't see how to avoid trigonometry to compute the angle, a verification by computation would not be very convincing. Nevertheless we can proceed to an experimental verification with what's available. We "recover" the angle of two faces between the arms of a compass and then we measure it with a protractor; it's just an approximate verification, but one can reach an outstanding precision taking into account the rudimentary means used.


home page
French 		convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects January 2010
updated 30-03-2010