drawing in perspective

Representing an object of the space in a plane by giving the illusion of the third dimension is a real challenge!


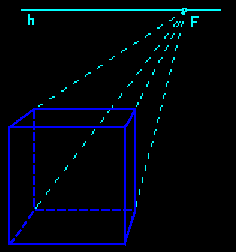
On a drawing in perspective (or a picture, here the railway of bay of the Somme - France), parallel lines contained in a plane parallel to the front plane are parallel , but other parallel lines converge on a vanishing point F on the horizon line h.		In parallel perspective all real parallel lines are also parallel on the drawing (vanishing point at the infinity).

To achieve a drawing geometrically useful, we have to respect a few elementary rules: preservation of alignment, of parallelism and of the midpoints. Such a drawing allows then to study affine properties, but not metric ones (angles and length are not preserved). To study metric properties (angles, orthogonality, length) we must use an orthographic projection, and thus chose its different parameters:
• a frontal plane (F): a segment in this plane or in a parallel plane is represented in real size (see remark below),
• a leak angle (a=30° on the picture): the lines perpendicular to (F), the vanishing lines, are represented in this direction,
• a reduction ratio (k=0.5 on the picture): the lengths represented in the vanishing direction are multiplied by k.
The point (x, y, z) of the space is thus represented with the point (x + y×k×cos[a], z + y×k×sin[a]) of the plane (F)=(xOz).
We choose for (F) a plane linked to the object which will be represented, then a<45° and r=0.5 (these values give a nice look).

To depict some line (neither parallel nor perpendicular to the frontal plane) we must determine two of its points or one of its points and its direction (a parallel line). Let's notice that the representation of a circle is usually an ellipse.
To improve the readability of the representation the hidden parts are drawn with dotted lines.

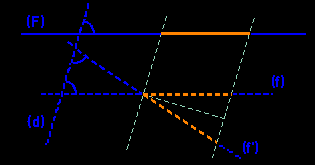
Remark: in a parallel perspective distances are preserved in the planes parallel to the frontal plane (F), but there is another plane direction where this property holds: the direction (f') symmetric of the one (f) of the frontal plane with respect to the projection direction (d).
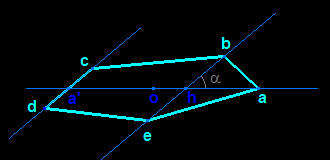
Indeed, among the quadrilaterals with two parallel sides and two sides with same length one finds, besides the parallelogram, the isosceles trapezium and crossed types.

To improve your knowledge: La perspective cavalière (Audibert G.) - APMEP 1990 (in French)

Now we are ready to achieve some nice drawings using simple constructions!

let's cut a cube

The cutting plane is defined by three points laying on three edges.
The constructions are easy; they use the preservation of the alignment and of the parallelism (two parallel planes determine two parallel lines on a secant plane). The elements in the section plane are represented in green, the section polygon in red.
In the two last cases we have to use an intersection point (external to the cube) of the section plane with an edge.
The "little" pigeon holes theorem allows us to foresee the different possible cases. The six faces are shared by pairs in three directions two by two orthogonal; the sides of the section polygon can thus only belong to three directions (the holes), each of them containing no more than two sides ("little" holes). So a section can be a triangle, a quadrilateral (trapezium or parallelogram), a pentagon (with two pairs of parallel sides) or an hexagon (with opposite sides parallel).

cuttings of a cube

Drawing the section polygon in real size needs a little more work, but remains an elementary exercise. The sides laying in the front and back panes are in real size; the segments laying on vanishing lines have real size double of those appearing on the drawing (for a ratio r=1/2). Thus we can, using constructions of well chosen rectangular triangles, obtain the length of all segments whose ends lay on two perpendicular edges.
To restrict the number of length to construct, we may notice that a section is always either a parallelogram, either a parallelogram truncated by a line (triangle, trapezium, pentagon) or by two parallel lines (hexagon).

exercises: Can the section polygon be an equilateral triangle? a rectangle? a rhombus? a square? a regular pentagon? a regular hexagon?
It is of course advisable to look for answers with arguments before to consult the solutions.

two simple examples of drawings in parallel perspective

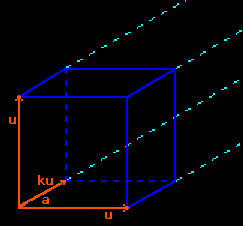
It is important to understand how these two drawings are made; we choose a leak angle α=40° and a reduction ratio k=0.5=1/2.

parallel perspective of a cube with a diagonal plane as frontal plane

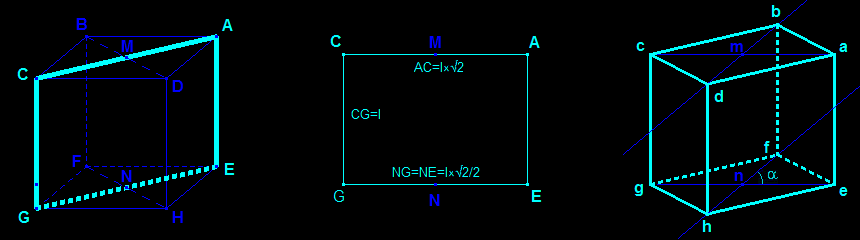
Here the frontal plane is imposed; it therefore contains two opposite edges [AE] and [CG] (with length l) and two parallel diagonals [AC] and [EG] of opposite faces of the cube ABCDEFGH. Let us first examine the face ABCD of the cube: its diagonals [AC] and [BD] are perpendicular and have the same midpoint M, thus MA=MB=MC=MD=(l√2)/2. The section rectangle ACGE is seen in real size: l × l√2.

parallel perspective (cube)

Let us begin by drawing the rectangle acge; we can now place the midpoints m of [ac] and n of [ge]. It remains to place the four missing vertices: since (AC)⊥(BD), b and d are on the vanishing lines passing through m and such that mb=md=l×√2/4, and similarly for f and h on the vanishing lines passing through n. All that remains is to draw the cube abcdefgh.

parallel perspective of a regular pentagon

Since the pentagon is a plane figure, its plane can not serve as a frontal plane (no deformation); thus we choose a pertinent orthogonal plane containing an "interesting element", for example one of its symmetry axes; with this choice one side and the opposite diagonal lay in the vanishing direction.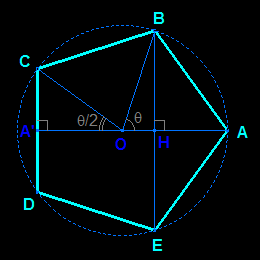
On the drawing of a regular pentagon inscribed in a circle of radius r=1 (let us be simple!) let us determine the lengths necessary for the drawings. The angle between two successive radii is θ=72 °; thus we shall use elementary trigonometry.

OH = cosθ ≈ 0,31
OA' = cos(θ/2) ≈ 0,81
HB = HE = sinθ ≈ 0,95
A'C = A'D = sin(θ/2) ≈ 0,59

parallel perspective of the regular pentagon

The front plane contains the axis of symmetry aa' and is orthogonal to the segment CD. We can place on it o, a such that a=OA=r=1, a' such that oa'=OA' and h such that oh=OH. c and d are on the vanishing line passing through a' and such that a'c=a'd=A'C/2, and b and e are on the vanishing line passing through h and such that hb=he=HB/2. All that remains is to draw the pentagon abcde.

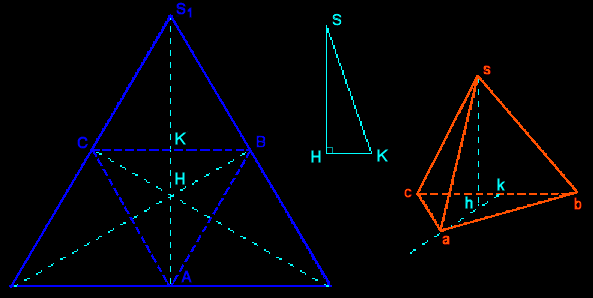
let's draw a parallel perspective of a regular tetrahedron

The most easiest is to use four vertices of a cube; we obtain a nice drawing, but not very practical.
Otherwise we use the net (equilateral triangle with its midpoints triangle). The orthocenter H of the base ABC is also center of gravity and orthogonal projection of the vertex S on the plane (ABC). We can easily construct the altitude HS of the pyramid.

Let us now choose the elements of the perspective: the frontal plane containing [BC] and perpendicular to the plane (ABC), the vanishing direction (the altitude (AK) of ABC is a vanishing line), and the reduction ratio 1/2.
First we construct the altitude HS in real size. Then we place successively b and c (bc=BC), k midpoint of [bc]. On the vanishing line (ka) we place a such as ka=KA/2 and h such as kh=KH/2=ka/3. Finally we have to place s on the line perpendicular to (bc) going through h, such as hs=HS.

Exercise: Achieve a drawing using a plane of symmetry (containing an edge and the midpoint of the opposite edge) as frontal plane.

let's draw a parallel perspective of a tetrahedron using its net

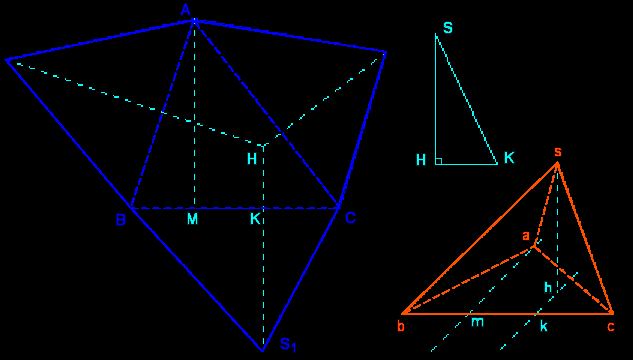
H is the orthogonal projection of the vertex S on the base plane (ABC). (MA) is one altitude of ABC. We construct the altitude SH in real size.

[BC] lays in the frontal plane; (AM) and (KH) are vanishing lines.
We place successively b and c (bc=BC), m (bm=BM) and k (ck=CK). On two vanishing lines we place a such as ma=MA/2 and h such as kh=KH/2. Finally we place s such as hs=HS on the line perpendicular to (bc) going through h.

drawings of regular polygons in perspective

We use the interesting elements of a construction in real size, and choose the frontal plane in a way to have vanishing lines which allow us to place the other vertices.

polygon (polyhedra)

element(s) in the frontal plane

fuyante(s)

equilateral triangle (regular tetrahedron, prism)	- one side - one altitude	- one altitude - one side
square (cube, octahedron, antiprism, pyramid)	- one side - one diagonal	- two sides - the other diagonal
pentagon (prism, pyramid, antiprism)	- one axis of symmetry	- one diagonal and one side
hexagon (prism, pyramid, antiprism)	- one non diagonal axis of symmetry - one great diagonal	- one great diagonal and two sides - two small diagonals
octagon (prism, pyramid, antiprism)	- one axis of symmetry	- two medium diagonals and two sides

Here we are ready to draw some polyhedra!

correction of the effects of perspective in architecture

The perspective "distorts", in particular buildings; so that they appear as they are, it must therefore be tricky. The Parthenon is a fine example of the tricks implemented by architects to correct these distortions:
• swollen columns and more or less inclined towards the inside,
• thicker corner columns,
• domed base, treads and pediment curved.
The drawing shows the monument as it appears to us and its appearance in the absence of "correction". Each block of stone is therefore unique, cut to the nearest millimeter, according to its place in the building. With the techniques of the time, this feat was achieved in just nine years.

references (in French):

• artips : au millimètre près (in French)
• passerelle(s) : des déformations intentionnelles

home page

convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects

August 1999
updated 25-06-2020