dessiner en perspective cavalière

Représenter un objet de l'espace sur un plan en donnant l'illusion de la troisième dimension est un vrai défi !


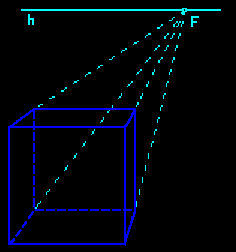
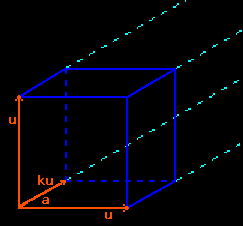
Sur un dessin en perspective (ou une photo, ici le chemin de fer de la Baie de Somme) les parallèles contenues dans un plan parallèle au plan frontal sont parallèles, mais les autres parallèles sont concourantes en un point de fuite F sur la ligne d'horizon h.		En perspective cavalière, toutes les parallèles réelles sont aussi parallèles sur le dessin (point de fuite à l'infini).

Pour réaliser un dessin exploitable géométriquement, il faut respecter quelques règles élémentaires : conservation de l'alignement, du parallélisme et des milieux. Un tel dessin permet alors d'étudier des propriétés affines, mais pas métriques (les angles et les longueurs ne sont pas conservés). Pour étudier des propriétés métriques (angles, orthogonalité, longueurs) il faut utiliser une perspective cavalière, et donc choisir ses différents paramètres :
• un plan frontal (F) : un segment contenu dans ce plan ou dans un plan parallèle est représenté en vraie grandeur (voir remarque),
• un angle de fuite (a=30° sur la figure) : les perpendiculaires à (F), les fuyantes, seront représentées dans la direction ainsi définie,
• un coefficient de réduction (k=0,5 sur la figure) : les longueurs représentées dans la direction de fuite sont multipliées par k.
Le point (x, y, z) de l'espace est donc représenté par le point (x + y×k×cos[a], z + y×k×sin[a]) du plan (F)=(xOz).
On choisit pour (F) un plan lié à l'objet que l'on désire représenter, puis a<45° et r=0,5 (ces valeurs donnent un bel aspect).

Pour représenter une droite "quelconque" (ni parallèle ni perpendiculaire au plan frontal) il faut déterminer deux de ses points ou un de ses points et sa direction (une droite parallèle). Notons que la représentation d'un cercle est généralement une ellipse.
Pour améliorer la lisibilité de la représentation on trace les parties cachées en pointillés.

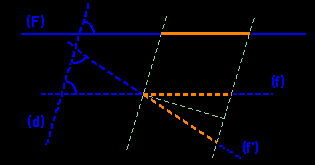
Remarque : dans une perspective cavalière les distances sont préservées dans les plans parallèles au plan frontal (F), mais il existe une autre direction de plans où cette propriété a lieu : la direction (f') symétrique de celle (f) du plan frontal par rapport à la direction de projection (d).
En effet, parmi les quadrilatères avec deux côtés parallèles et deux côtés de même longueur on trouve, outre le parallélogramme, le trapèze isocèle et des types croisés.

Pour approfondir vos connaissances : La perspective cavalière (Audibert G.) - APMEP 1990

Nous voilà parés pour réaliser quelques jolis dessins à l'aide de constructions simples !

coupons un cube

Le plan de coupe est défini par trois points choisis sur trois arêtes.
Les constructions sont faciles ; elles utilisent la conservation de l'alignement et du parallélisme (deux plans parallèles déterminent sur un plan sécant deux droites parallèles). Les éléments du plan de coupe sont représentés en vert, le polygone de coupe en rouge.
Dans les deux derniers cas il faut utiliser un point d'intersection (extérieur au cube) du plan de coupe avec une arête.
Le théorème des "petits" tiroirs permet de prévoir les différents cas possibles. Les six faces sont réparties par paires dans trois directions deux à deux orthogonales ; les côtés du polygones de coupe ne peuvent donc appartenir qu'à trois directions (les tiroirs), chacune d'elles ne pouvant contenir plus de deux côtés ("petits" tiroirs). Ainsi une coupe peut être un triangle, un quadrilatère (trapèze ou parallélogramme), un pentagone (avec deux paires de côtés parallèles) ou un hexagone (avec les côtés opposés parallèles).

coupes d'un cube

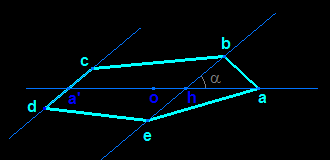
Dessiner en vraie grandeur le polygone de coupe demande un peu plus de travail, mais reste un exercice élémentaire. Les côtés situés dans les faces avant (plan frontal) et arrière sont en vraie grandeur ; les segments dont les supports sont des fuyantes ont des longueurs réelles doubles de celles apparaissant sur le dessin (pour un coefficient r=1/2). On peut donc, à l'aide de constructions de triangles rectangles bien choisis, obtenir les longueurs de tous les segments dont les extrémités appartiennent à deux arêtes perpendiculaires.
Pour limiter le nombre de longueurs à construire, on peut remarquer qu'une coupe est toujours soit un parallélogramme, soit un parallélogramme tronqué par une droite (triangle, trapèze, pentagone) ou par deux droites parallèles (hexagone).

exercices : Le polygone de coupe peut-il être un triangle équilatéral ? un rectangle ? un losange ? un carré ? un pentagone régulier ? un hexagone régulier ?
Il convient évidemment de chercher des réponses argumentées avant de consulter les solutions.

deux exemples simples de dessins en perspective cavalière

Il est important de bien comprendre comment ces deux dessins sont réalisés ; nous choisissons un angle de fuite α=40° et un coefficient de réduction k=0,5=1/2.

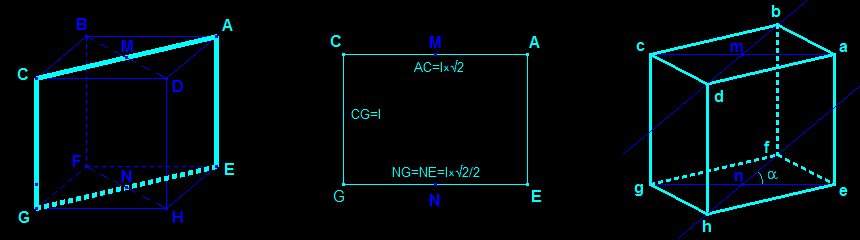
perspective cavalière d'un cube avec un plan diagonal comme plan frontal

Ici le plan frontal est imposé ; il contient donc deux arêtes opposées [AE] et [CG] (de longueur l) et deux diagonales parallèles [AC] et [EG] de faces opposées du cube ABCDEFGH. Examinons d'abord la face ABCD du cube : ses diagonales [AC] et [BD] sont perpendiculaires et ont même milieu M, donc MA=MB=MC=MD=(l√2)/2. Le rectangle de coupe ACGE est vu en vraie grandeur : l × l√2.

perspective cavalière (cube)

Commençons par dessiner le rectangle acge ; nous pouvons maintenant placer les milieux m de [ac] et n de [ge]. Il reste à placer les quatre sommets manquants : puisque (AC)⊥(BD), b et d sont sur la fuyante passant par m et tels que mb=md=l×√2/4, et de même pour f et h sur la fuyante passant par n. Il ne reste qu'à tracer le cube abcdefgh.

perspective cavalière d'un pentagone régulier

Le pentagone étant une figure plane, son plan ne peut servir de plan frontal (pas de déformation) ; on choisit donc un plan orthogonal pertinent contenant un "élément intéressant", par exemple un des axes de symétrie du pentagone ; avec ce choix un côté et la diagonale opposée sont dans la direction de fuite.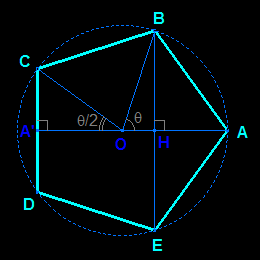
Sur le dessin d'un pentagone régulier inscrit dans un cercle de rayon r=1 (soyons simple !) déterminons les longueurs nécessaires au dessin. L'angle entre deux rayons successifs est θ=72° ; nous utiliserons donc la trigonométrie élémentaire.

OH = cosθ ≈ 0,31
OA' = cos(θ/2) ≈ 0,81
HB = HE = sinθ ≈ 0,95
A'C = A'D = sin(θ/2) ≈ 0,59

perspective cavalière du pentagone régulier

Le plan frontal contient l'axe de symétrie (aa') et est orthogonal à (DC). On peut y placer o, a tel que oa=OA=r=1, a' tel que oa'=OA' et h tel que oh=OH. c et d sont sur la fuyante passant par a' et tels que a'c=a'd=A'C/2, et b et e sont sur la fuyante passant par h et tels que hb=he=HB/2. Il ne reste qu'à tracer le pentagone abcde.

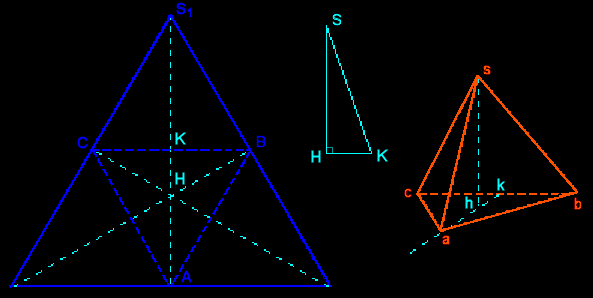
dessinons une perspective cavalière d'un tétraèdre régulier

Le plus simple consiste a utiliser quatre sommets d'un cube ; on obtient un joli dessin, mais peu pratique.
Sinon, on utilise le patron (triangle équilatéral avec son triangle des milieux). L'orthocentre H de la base ABC est aussi centre de gravité et projection orthogonale du sommet S sur le plan (ABC). On peut facilement construire la hauteur HS de la pyramide.

Choisissons maintenant les éléments de la perspective cavalière : le plan frontal contenant [BC] et perpendiculaire au plan (ABC), la direction de fuite (la hauteur (AK) de ABC est une fuyante), et le rapport de réduction 1/2.
On construit d'abord la hauteur SH en vraie grandeur. Puis on place successivement b et c (bc=BC), k milieu de [bc]. Sur la fuyante (ka) on place a tel que ka=KA/2 et h tel que kh=KH/2=ka/3. Il ne reste plus qu'à placer s sur la perpendiculaire à (bc) passant par h, tel que hs=HS.

Exercice : Réalise un dessin en utilisant un plan de symétrie (contenant une arête et le milieu de l'arête opposée) comme plan frontal.

dessinons une perspective cavalière d'un tétraèdre à partir de son patron

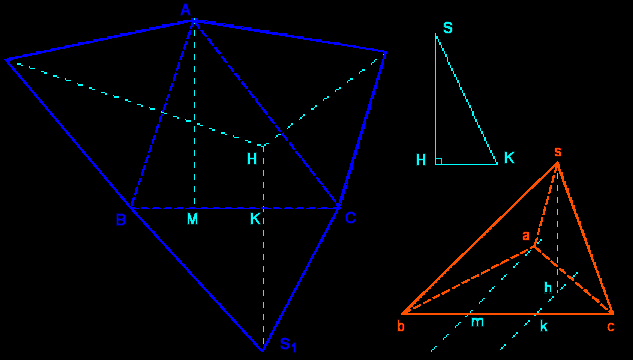
H est la projection orthogonale du sommet S sur le plan de base (ABC). (MA) est une hauteur de ABC. On construit la hauteur SH en vraie grandeur.

Le plan frontal contient [BC] ; (AM) et (KH) sont des fuyantes.
On place successivement b et c (bc=BC), m (bm=BM) et k (ck=CK). Sur deux fuyantes on place a tel que ma=MA/2 et h tel que kh=KH/2. Enfin, on place s tel que hs=HS sur la perpendiculaire à (bc) passant par h.

dessins de polygones réguliers en perspective cavalière

On utilise les éléments intéressants d'une construction en vraie grandeur, et on choisit le plan frontal de manière à disposer de fuyantes permettant de placer les sommets manquants.

polygone (polyèdres)

élément(s) du plan frontal

fuyante(s)

triangle équilatéral (tétraèdre régulier, prisme)	- un côté - une hauteur	- une hauteur - un côté
carré (cube, octaèdre, antiprisme, pyramide)	- un côté - une diagonale	- deux côtés - l'autre diagonale
pentagone (prisme, pyramide, antiprisme)	- un axe de symétrie	- un côté et une diagonale
hexagone (prisme, pyramide, antiprisme)	- un axe de symétrie non diagonal - une grande diagonale	- une grande diagonale et deux côtés - deux petites diagonales
octogone (prisme, pyramide, antiprisme)	- un axe de symétrie	- deux diagonales moyennes et deux côtés

Nous voilà parés pour dessiner quelques polyèdres !

corrections des effets de la perspective en architecture

La perspective "déforme", en particulier les bâtiments ; pour qu'ils apparaissent tels qu'ils sont, il faut donc ruser. Le Parthénon est un bel exemple des astuces mises en œuvre par les architectes pour corriger ces déformations :
• colonnes renflées et plus ou moins inclinées vers l'intérieur,
• colonnes d'angle plus épaisses,
• base bombée, marches et fronton incurvés.
Le dessin montre le monument tel qu'il nous apparaît et son apparence en l'absence de "correction". Chaque bloc de pierre est donc unique, taillé au millimètre près, selon sa place dans l'édifice. Avec les techniques de l'époque, cet exploit a été réalisé en seulement neuf ans.

références :

• artips : au millimètre près
• passerelle(s) : des déformations intentionnelles

page accueil

polyèdres convexes - polyèdres non convexes - polyèdres intéressants - sujets connexes

août 1999
mis à jour 25-06-2020