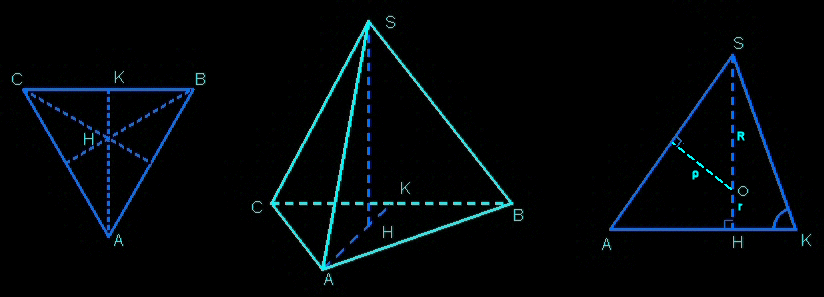
dans un tétraèdre régulier

Commençons par dessiner un tétraèdre régulier en perspective cavalière, et examinons-le pour y repérer les éléments dont nous aurons à calculer les mesures. tétraèdre régulier
Pour une raison de symétrie le projeté orthogonal H de S sur le plan (ABC) est le centre du triangle équilatéral ABC ; il est donc situé aux deux tiers de la médiane [AK], soit AH=(2/3)AK et KH=AK/3
Une bonne façon de procéder consiste à se ramener dans un plan en pratiquant une coupe pertinente dans le polyèdre. Ici le plan (ASH) s'impose : il contient la hauteur [SH] de la pyramide et les côtés [KA) et[KS) de l'angle de deux faces.
Avant de commencer les calculs, rappelons que
  •   la hauteur d'un triangle équilatéral de côté a égale a×√3/2, donc avec BC=a, KA=KS=a×√3/2,
  •   le volume d'une pyramide égale le tiers du produit de l'aire de la base par la hauteur.
Hauteur SH=h (théorème de Pythagore dans le triangle ASH rectangle en H) :  SH²= SA²-AH²= a²-[(2/3)×a×√3/2]²= (1-1/3)×a²= (2/3)×a²= h²  soit  h=(√2/√3)×a
Aire de ABC :  (1/2)×BC×AK = (1/2)×a×(a×√3/2) = (√3/4)×a²
Volume du tétraèdre :  (1/3)×[(√3/4)×a²]×[(√2/√3)×a] = (√2/12)×a³
Angle de deux faces :  cosθ = KH/KS = (a√3/6)/(a√3/2) = 1/3   d'où   θ ≈ 70,53° ≈ 70°32'

Ces résultats ne sont ni évidents, ni connus par cœur (sauf de quelques génies !) ; il convient donc de les vérifier.

On peut recalculer le volume en utilisant le cube dans lequel le tétraèdre s'inscrit naturellement.
La diagonale d'une face égale a (arête du tétraèdre), d'où l'arête du cube c=a/√2.
Pour obtenir le tétraèdre il faut couper quatre "coins" du cube (tétraèdres trirectangles à base équilatérale). Si on utilise une des faces isocèles-rectangles comme base, la hauteur d'un "coin" est alors c, et son volume   (1/3)×(c²/2)×c = c³/6
on en déduit le volume du tétraèdre : c³-4(c³/6) = c³/3 = (a/√2)³/3 = (√2/12)×a³
Corollaire 1 : La hauteur des tétraèdres trirectangles relative à la face équilatérale est le tiers de la diagonale du cube d=c√3.
preuve : de   V = (1/3)×A×h   on tire   h = 3V/A = 3[c³/6]/[(1/2)×(c√2)×(c√2)(√3/2)] = c/√3 = c√3/3 = d/3
Corollaire 2 : La sphère circonscrite (définie par les quatre sommets) est, par symétrie, centrée au point d'intersection des hauteurs ; son centre O est situé au quart de chaque hauteur (à partir de la base), son rayon est donc  R = (3/4)×h = (√6/4)×a
preuves : •  O est l'isobarycentre des sommets  O = bar[A(1),B(1),C(1),S(1)] = bar[bar[A(1),B(1),C(1)],S(1)] = bar[H(3),S(1)]  situé au quart de [HS]
               •  On peut aussi utiliser le cube dont quatre sommets définissent le tétraèdre ; les deux polyèdres ont même sphère circonscrite.
Une hauteur du tétraèdre et une diagonale du cube ont même support et  h=(2/3)d  donc  R = d/2 = 1/2×(3/2)h = (3/4)×h
vérification : a=c√2, d=c√3 et h=(2/3)d  d'où  R = d/2 = (3h/2)/2 = (3/4)×h  ou  R = (c√3)/2 = ((a/√2)√3)/2 = a×(√6/4) = a(√2/√3)×(3/4) = h×(3/4)
remarques : rayon de la sphère inscrite (tangente aux faces, centre O) : r = h/4 = R/3 = a×(√6/12)
                    rayon de l'intersphère (tangente aux arêtes, centre O) : par le théorème de Pythagore  ρ² = R²-(a/2)² d'où  ρ = a(√2/4)

Puisqu'on ne voit pas comment se passer de la trigonométrie pour calculer l'angle, une vérification par le calcul ne serait pas bien convaincante. On peut néanmoins procéder à une vérification expérimentale avec les moyens du bord. On "récupère" l'angle de deux faces entre les branches d'un compas puis on le mesure avec un rapporteur ; ce n'est qu'une vérification approchée, mais on peut arriver à une étonnante précision, compte tenu des moyens rudimentaires utilisés.


page accueil
anglais 		polyèdres convexes - polyèdres non convexes - polyèdres intéressants - sujets connexes janvier 2010
mis à jour 30-03-2010