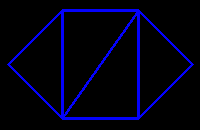
net of the tetrahedra (four right triangles)
folded in two ways it gives two mirror image tetrahedra
lengths of the edges: a, a√2, a√3
(the midpoint of the longest is the center of the circumsphere)
If it is not possible to fill the space with regular tetrahedra, we nevertheless can carry out periodic pavings with others polyhedra among which the Hill's tetrahedra.
|
|
Construction: on the three lines orthogonal to the plan of an equilateral triangle AA1A2 and going through its vertices we put three points B, C and D such as A1B=h, A2C=2h and AD=3h.
(ABCD) is a Hill's tetrahedron (type 1); it has a symmetry axis defined by the midpoints E and F of [AD] and [BC]. By cutting it in two "halfs" with the planes (BCE) and (ADF) we get two others Hill's tetrahedra (types 2 and 3): (ABCE) and (ABDF). |
|
| Here is an elegant dissection of a Hill's tetrahedron of type 1 (Scöbi and Hanegraaf - 1985).
We decompose the tetrahedron into three polyhedra (two tetrahedra and an hexahedron) with which we reconstruct un right triangular prism with equilateral base (here two rotations suffice). Thus a dissection is a "puzzle" common to the two polyhedra: Hill's tetrahedron ↔ {P4, P6, P4'} ↔ triangular prism. |
|
The third Hilberts' problem (1900): given two tetrahedra with same base's area and same altitude (thus same volume), is it always possible to cut the first into finitely many polyhedral pieces which can be reassembled to yield the second?
In fact Hilbert doesn't spoke about it during his famous conference; Max Dehn just showed that the answer is no!
To prove that the regular tetrahedron is not equidecomposable with the cube of same volume Dehn associated to each polyhedron an invariant. More generally Jean-Pierre Sydler proved in 1985 that two polyhedra are equidecomposable if and only if the have same volume and same Dehn's invariant.
Dehn's invariant is a number δ(P) which depends only on the edges of the polyhedra P, more precisely on their lengths λi and the dihedral angles αi of the two faces which intersect at the edge with index i.
• δ is additive for the lengths and the angles: if P is decomposed into n polyhedra Pk then δ(P) is the sum of the n δ(Pk)
• δ(P) = Σ λi×f(αi) for the set of the edges of P, where f is a Q-linear function such as f(π)=0
(this last condition allows to add a face's diagonal as edge without modifying δ(P) because the corresponding dihedral angle is π)
In 1980 Debrunner proved that the Dehn's invariant of a polyhedron which periodically fills the space is null (like the one of the cube).
decomposition of the cube into six Schläflis' birectangular tetrahedra

net of the tetrahedra (four right triangles) folded in two ways it gives two mirror image tetrahedra lengths of the edges: a, a√2, a√3 (the midpoint of the longest is the center of the circumsphere) |
|
| references: |
• definitions of Hill's tetrahedra and dissections by Izidor Hafner
• Dehn's invariant • Décomposition des polyèdres et le troisième problème de Hilbert by Jean Lefort (in French) |
home page
 |
convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects | July 2012 updated 30-07-2012 |