
There are two circles tangent (one internally and the other externally) to three mutually tangent circles: the Soddy's circles which he has nicely named "kissing circles". The bends (signed reciprocals of the radii) of these two quadruplets satisfy the above Descartes' formula. One can iterate the construction with the new circles and create others quadruplets...
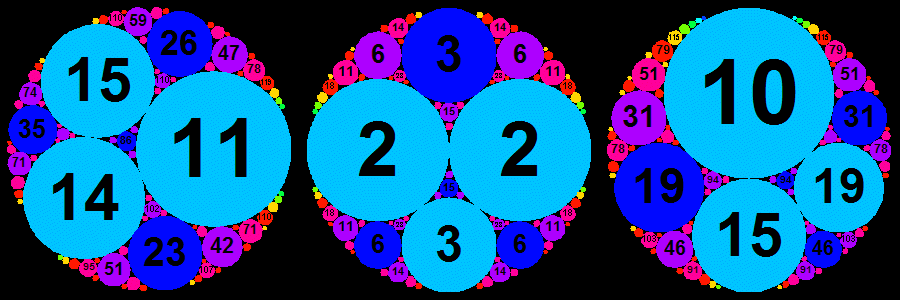
In the outstanding configurations below all the bends are integers, and the disks of same color belong to a same generation. There are other such configurations; how many? an infinity?
Remark: for the configuration on the left for example, Descartes' formula gives an easy way to find the bends 86 and -6 of the Soddy's circles of the first three circles (11,14,15); the outside circle has radius 1/6 and its curvature is negative because it contains the three circles.

A special case: "frieze of integers" (the two horizontal lines are circles with curvature zero).
One can go from one configuration to another by an appropriate inversion.
All the configurations with integer bends can be obtained with inversions of the "frieze of integers".
In the space there is a similar result which leads to quintuplets of mutually tangent spheres: the "kissing spheres". The relationship between the bends of the five spheres is different.
Remark: in a space with dimension n the bends ci of (n+2) hyperspheres, where each osculate with the (n+1) others, satisfy the relation n(Σci²)=(Σci)².
Nicolas Hannachi proved recently that there are an infinity of packings with integer bends which are topologically isometric; we can get them by inversions of Soddy's "bowl of integers". But we discovered more (see the section "carpet").
More details and superb images on Nicolas' page (in French).
Here are four configurations with integer bends, each defined by its root, the first "kiss" (four mutually tangent spheres).
(-1,2,2,3): the well known Soddy's "bowl of integers"( symmetry group D6h )
(-11,21,25,27) : "bingo", the first configuration discovered by Nicolas Hannachi
(-3,6,7,7) and (-2,3,6,7) : two others symmetric configurations from Nicolas ( groups C3v and C6v )
The spheres of a same generation are colored with the same color: successively cyan, blue, magenta, red yellow, green, ...
The packings (-1,2,2,3) and (-2,3,6,7) have been generated starting with a "hexlet" (see next section); we can generate and color (-11,21,25,27) and (-3,6,7,7) in the same way, but the coloring of (-3,6,7,7) then loses its symmetry.
The links above open pop-up windows with animations (successive generations and Nicolas' graphs of tangency).
Minimize the main window to better view these animations; only the pop-up windows will remain visible.
If your connexion is slow please be patient during the initialization ... the time for a long kiss!
|
|
|
If we consider two tangent spheres (blue) inscribed in a sphere (grey), there exist a ring of six externally tangent spheres (red) and tangent to these three spheres. The bends of these six spheres satisfy the relationship above.
Remark: A hexlet appears obviously in the "bowl of integers" and in (-2,3,6,7); these two configurations have a 6-axis of symmetry. But in fact all configurations contain an infinity of hexlets (see at the end of the section "carpet" below).
|
|
|
|
|
|
What is that "carpet"? Simply a spheres' packing between two parallel planes (which can be considered as two spheres with bend zero) ; the root of this new configuration is thus (0,0,1,1). The carpet is infinite, but it has the "kisses" and the 6-fold symmetry of the "bowl of integers"; its symmetry group is a6×C2
With "carpet of integer" we have discovered the common ancestor of all spheres' packings: with an appropriate inversion one can change the carpet into any configuration with integer bends. The applet shows "carpet of integers" with the inversion (yellow sphere) which changes it into "bowl of integers".
|
|
two animations: carpet <-> bowl and carpet <-> bingo Be patient during the initialization ... 600 Kb file!
a well hidden hexlet and an infinite sequence of hexlets
The images below should ought you to visit the "kissing pages" by Nicolas Hannachi (in French).
Here is the video (0:50 - 3.2 Mb) from which these images are extracted. An other version is also visible on Youtube.

 |
 |
 |
|
| references: |
• pages that can't be ignored: "disk packing " on the site math à mâter by Nicolas Hannachi (in French)
• Soddy circles, tangent spheres and bowl of integers on MathWorld (Eric W. Weisstein) • Circle Game (paper in Science News, April 2001) • The Kiss Precise, the poem devoted by Frederick Soddy to its "kissing circles" and "kissing spheres" • Jos Leys' wonderful tangent spheres de Jos Leys |
| The applets of this page have been achieved with Mathematica thanks to the research and coding work by Nicolas Hannachi. | |
home page
 |
convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects | March 2006 updated 24-03-2008 |