
Il existe deux cercles tangents (l'un intérieurement et l'autre extérieurement) à trois cercles mutuellement tangents : ce sont les cercles de Soddy qu'il a joliment appelé "kissing circles". Les courbures (inverses des rayons) des cercles de ces deux quadruplets vérifient la relation de Descartes ci-dessus. On peut itérer la construction en utilisant les nouveaux cercles et créer d'autres quadruplets...
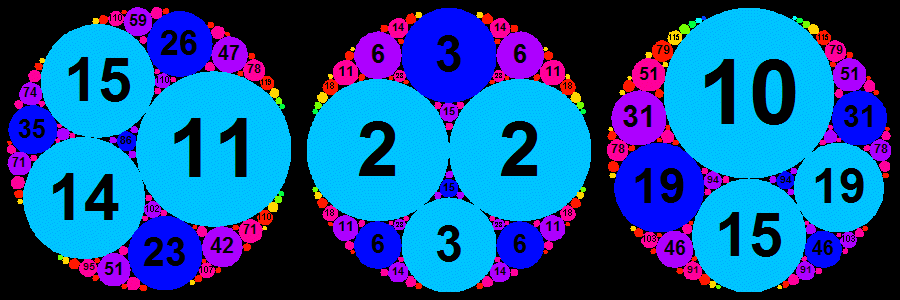
Dans les configurations remarquables ci-dessous toutes les courbures sont entières et les disques de même couleur appartiennent à une même génération. Il existe d'autres configurations de ce type ; combien ? une infinité ?
Remarque : pour la configuration de gauche par exemple, la relation de Descartes permet de trouver facilement les courbures 86 et -6 des cercles de Soddy des trois premiers cercles (11,14,15) ; le cercle extérieur a comme rayon 1/6, et sa courbure est négative puisqu'il contient les trois cercles.

Un cas particulier : "frieze of integers" (les deux droites horizontales sont des cercles de courbure nulle).
On peut passer d'une configuration à une autre par une inversion bien choisie.
Toutes les configurations peuvent être obtenues par inversions de la "frieze of integers".
Dans l'espace on a un résultat similaire qui conduit à des quintuplets de sphères mutuellement tangentes : les "kissing spheres". La relation entre les courbures des cinq sphères est différente.
Remarque : dans un espace de dimension n, les courbures ci de (n+2) hypersphères qui s'embrassent deux à deux vérifient la relation n(Σci²)=(Σci)².
Nicolas Hannachi a prouvé récemment qu'il existe une infinité de "packings" à courbures entières qui sont topologiquement isomorphes ; on peut les obtenir par des inversions du "bowl of integers" de Soddy. Mais on a découvert davantage ! (voir la partie "carpet").
Davantage de détails et de superbes images sur la page de Nicolas.
Voici quatre configurations à courbures entières, définies chacune par une souche, le premier "kiss" (quatre sphères mutuellement tangentes).
(-1,2,2,3) : le célèbre "bowl of integers" de Soddy ( groupe d'isométries D6h )
(-11,21,25,27) : "bingo", la première configuration découverte par Nicolas Hannachi
(-3,6,7,7) et (-2,3,6,7) : deux autres configurations symétriques découvertes par Nicolas ( groupes C3v et C6v )
Les sphères d'une même génération sont coloriées avec la même couleur : successivement cyan, bleu, magenta, rouge, jaune, vert, ...
Les packings (-1,2,2,3) et (-2,3,6,7) ont été générés à partir d'un "hexlet" (voir partie suivante) ; on peut générer et colorier (-11,21,25,27) et (-3,6,7,7) de la même manière, mais le coloriage de (-3,6,7,7) perd alors sa symétrie.
Les liens ci-dessus ouvrent chacun une fenêtre pop-up avec deux animations (générations successives et graphes de tangence de Nicolas).
Pour mieux voir ces animations minimisez la fenêtre principale ; seules les fenêtres pop-up resteront visibles.
Si votre connexion est lente soyez patients pendant l'initialisation ... le temps d'un long baiser !
|
|
|
Les ensembles des centres de familles de sphères fournissent encore une manière de créer de nouveaux polyèdres, mais leurs enveloppes convexes n'ont pas de propriétés intéressantes et ne sont pas très belles. Ce que nous appelons beauté d'un polyèdre n'est souvent qu'une façon de traduire la richesse de son groupe d'isométries.
Si l'on considère deux sphères tangentes (bleues) inscrites dans une sphère (grise), il existe un anneau de six sphères (rouges) tangentes extérieurement deux à deux et tangentes aux trois autres sphères (bleues et grise). Les courbures de ces six sphères satisfont aux relations ci-dessus.
Remarque : Un hexlet apparaît clairement dans le "bowl of integers" et dans (-2,3,6,7) ; ces deux configurations ont en effet un 6-axe de symétrie. Mais en fait toutes les configurations contiennent une infinité de hexlets (voir à la fin de la partie "carpet" ci-dessous).
|
|
|
|
|
|
Qu'est-ce que ce "tapis" ? Tout simplement un packing de sphères entre deux plans parallèles (que l'on peut considérer comme deux sphères de courbure zéro) ; la souche de cette nouvelle configuration est donc (0,0,1,1). Le tapis est infini, mais on y retrouve les "kiss" et la symétrie d'ordre six du "bowl of integers" ; son groupe d'isométries est a6×C2
Avec "carpet of integers" on a découvert l'ancêtre commun à tous les packings de sphères : avec une inversion convenable on peut transformer le tapis en n'importe quelle configuration à courbures entières. L'applet montre "carpet of integers" avec l'inversion (sphère jaune) qui le transforme en "bowl of integers".
|
|
deux animations : carpet <-> bowl et carpet <-> bingo Soyez patients pendant l'initialisation ... fichier de 600 Ko !
un hexlet bien caché et une suite infinie de hexlets
Les images ci-dessous devraient vous inciter à visiter les "kissing pages" de Nicolas Hannachi.
Voici la vidéo (0'50 - 3,2 Mo) d'où sont extraites ces images. Une version est aussi visible sur Youtube.

 |
 |
 |
|
| références : |
• des pages qu'on ne peut ignorer : "disk packing " sur le site math à mâter de Nicolas Hannachi
• Soddy circles, tangent sphere et bowl of integers sur MathWorld (Eric W. Weisstein), en anglais • Circle Game (article de Science News, avril 2001), en anglais • The Kiss Precis, le poème que Frederick Soddy a consacré à ses "kissing circles" et "kissing spheres" (en anglais) • les magnifiques sphères tangentes de Jos Leys |
| Les applets de cette page ont été réalisé avec Mathematica grâce au travail de recherche et de codage de Nicolas Hannachi. | |
page accueil
 |
polyèdres convexes - polyèdres non convexes - polyèdres intéressants - sujets connexes | mars 2006 mis à jour 24-03-2008 |