the inversion

An inversion IP,r is a geometric transformation of the plane (mapping: point M → point M') defined by PM'×PM=r² (notation: PM is the distance between P and M) where the three points P, M and its image M' are collinear (lying on a same line), with M and M' on the same side of the center P.
The point P doesn't have an image (when M comes close to P, its image M' speeds to infinity!).
The set of fixed points (such as M'=M) is obviously the circle with center P and radius r: it's the inversion circle.
The originality of this involution (bijection which is its own reciprocal: M → M' → M for every point M) is to transform a line not passing through P into a circle passing through P, and conversely. A line passing through P is globally invariant. A circle not passing through P is transformed into a circle; beware, the centers of the two circles are NOT inverse!
In an inversion angles are preserved (conformal mapping), thus a circle orthogonal to the inversion circle is globally invariant.
Treating lines as circles of infinite radius, all circles invert to circles. Furthermore, any two non intersecting circles can be inverted into themselves (each globally invariant), into concentric circles (with same center) or into isometric circles (with same radius).

pole and polar ("polar inversion") :
If A' is the inverse of A with respect to a circle, the polar of A is the perpendicular ΔA to the line AA' going through A'; and similarly the polar of A' is the perpendicular ΔA' to the line AA' going through A.

So a "line-grid" (white, deprived of its center P) is transformed into an "arc-grid" (red) composed of four half-lines and circles' arcs two by two orthogonal (the arcs belong to circles passing through P). The intersections of a segment and its image (arc) belong to the inversion circle (blue).

grid and its inverse
inverse of a line
(drag the big white points A and B) 		inverse of a circle
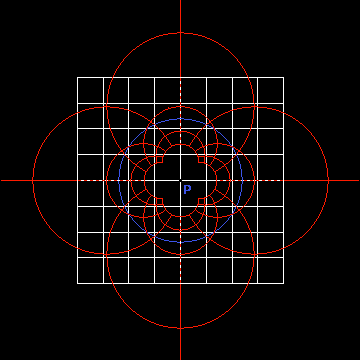
(drag the big white points C and M) 		inverse of a square grid

A nice example: the two images below show a chessboard superimposed with its inverse.
The external cirle/square just limits the size of the image; indeed the four external zones are the infinite images of the four central squares (one of their vertices is the center P). The central part is not colored in green/blue; it's the image of the outside of the chessboard.

chess and its inverse (in green) chess and its inverse (in blue)

The properties that inversion transforms circles and lines to circles or lines and that it preserves the angles makes it an extremely important tool of plane geometry: by choosing a suitable inversion circle it is often possible to transform one geometric configuration into another simpler one in which a proof is more easy.

The definition and the properties of the plane inversion remain true in the space: it suffices to replace "line" by "plane" and "circle" by "sphere".
Two nice applications: the duality of the polyhedra and the "kissing circles/spheres".

references: •  inversion - MathWorld
•  Éléments de géométrie - L'inversion  by Arnaud Bodin, in French
•  Inversion géométrique - ChronoMath  by Serge Mehl, in French
•  L'inversion  (Catholic University of Louvain - Belgium), in French
•  Ceci n'est pas une géodésique ! (hyperbolic line)  in French - PDF version

home page
French 		convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects August 2012
updated 02-09-2012