cutting a tetrahedron

The plan of the section is defined by three green points chosen on the solid's surface ; the lines laying in this plane are also drawn in green, while the section's polygon is in red. The tool of this type of construction is the preservation of alignment in a perspective (parallelism is also preserved, but not orthogonality).

If one of the points is chosen on an edge, or if two points are chosen on a same face:
•  when the section is triangular, none intermediate construction is needed to draw it,
•  when the section is a quadrilateral, we have to determine, using a line supporting an edge of the base, a second point to obtain the intersection line between the section's plane and the base plane. This line provides the fourth vertex J of the quadrilateral.

tetrahedron (5 cuts)

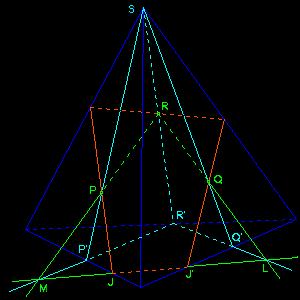
If the three points are chosen in three faces, we must determine the intersection line between the cutting and base planes, thus construct two points K and L of this line. The line (QR) meets the base plane in L which is determined using a second line (Q'R'), intersection between the plane (SQR) and the base plane.
•  If the line (KL) is outside of the base triangle, then an intersection point D with a line supporting an edge of the base allows to draw the line (PD) supporting one of the sides of the triangular section (point J); it is easy to finish to draw the triangle.
•  If the line (LM) meets two edges of the base, then these intersection points J and J' are two vertices of the quadrilateral section which can now be easily drawn.
We verify that R lays on the section's polygon, and that the line supporting the third side of P'Q'R' allows to define an other point on the intersection line between the plane (PQR) and the base plane.

tetrahedra (cut 1)
tetrahedra (cut 2)

home page
French 		convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects April 1999
updated 10-03-2001