
Si l'un des points est choisi sur une arête, ou si deux points sont choisis sur une même face :
• lorsque la coupe est triangulaire, aucune construction intermédiaire n'est nécessaire pour la tracer,
• lorsque la coupe est un quadrilatère, il faut déterminer, grâce au support d'une arête de base, un second point pour obtenir la droite d'intersection entre le plan de coupe et le plan de base. Cette droite fournit le quatrième sommet J du quadrilatère.

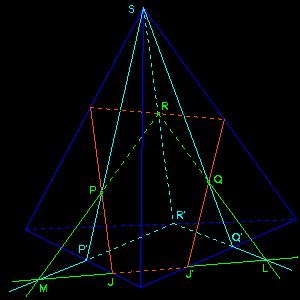
Si les trois points sont choisis dans trois faces, il faut déterminer la droite d'intersection entre les plans de coupe et de base, donc construire deux points K et L de cette droite. La droite (QR) coupe le plan de base en L que l'on détermine à l'aide d'une seconde droite (Q'R'), intersection du plan (SQR) et du plan de base.
• Si la droite (KL) est extérieure au triangle de base, alors un point d'intersection D avec une droite supportant une des arêtes de base permet de tracer le support (PD) d'un des côtés du triangle de coupe (point J) ; le tracé du triangle est facile à achever.
• Si la droite (LM) coupe deux arêtes de base, alors ces points d'intersection J et J' sont deux sommets du quadrilatère de coupe qui peut alors être tracé facilement.
On vérifie que R appartient au polygone de coupe, et que la droite support du troisième côté de P'Q'R' permet de définir un autre point sur la droite d'intersection du plan (PQR) avec le plan de base.
 |
|
 |
page accueil
 |
polyèdres convexes - polyèdres non convexes - polyèdres intéressants - sujets connexes | avril 1999 mis à jour 10-03-2001 |