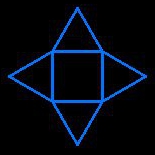
 antiprisme carré
antiprisme carré(on assemble deux pièces pour créer un anneau de triangles tête-bêche)
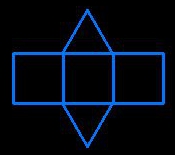 prisme triangulaire
prisme triangulaire 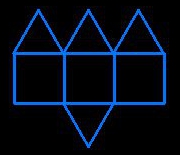 assemblage
assemblageprisme-tétraèdre
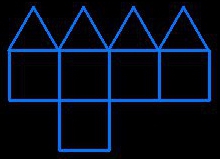 assemblage
assemblagecube-pyramide
• assemblages de triangles et de carrés
8 triangles et 2 carrés
 antiprisme carré
antiprisme carré(on assemble deux pièces pour créer un anneau de triangles tête-bêche) |
2 triangles et 3 carrés
 prisme triangulaire
prisme triangulaire |
4 triangles et 3 carrés
 assemblage
assemblageprisme-tétraèdre |
4 triangles et 5 carrés
 assemblage
assemblagecube-pyramide |
• ombres de polyèdres
Les polyèdres suivants peuvent produire une ombre carrée :• coupes d'un cube
• Pour obtenir un carré il faut utiliser un plan parallèle à une face.• un joli polyèdre équifacial
|
Le polyèdre a 24 faces identiques en forme de cerf-volant, chacune déterminée par une des 3x8 coupes. Ses arêtes et ses sommets appartiennent aux plans et axes de symétrie du cube.
Il y a des coupes transversales (en deux polyèdres symétriques) intéressantes : trois parallèles aux faces du cube qui sont des octogones réguliers, et quatre perpendiculaires aux diagonales du cube qui sont des hexagones réguliers. Son volume est le tiers de celui du cube (preuve détaillée). Patron à télécharger (A5 demi-patron). |
|