miscellaneous examples of convex polyhedra

Reminder: A polyhedron is convex if all its diagonals are inside or on its surface.
A diagonal of a polyhedron is a segment joining two vertices and which is not an edge.

the Goldberg's polyhedra

The convex polyhedra of this family described by Michael Goldberg in 1937 have only pentagonal and hexagonal faces with exactly three faces meeting at each vertex and they have icosahedral symmetry Ih or I  (with or without mirror symmetries). Such a polyhedron has necessarily 12 regular pentagonal faces.
proof: these polyhedra verify the Euler formula  f+v=e+2  with  f=f5+f6  Since 3 faces meet at each vertex we have  v=(5f5+6f6)/3   e=(5f5+6f6)/2  and the Euler formula gives then  f5=12
Remark: we show likewise that a convex polyhedron with square and hexagonal faces has necessarily 6 square faces.
We already know the truncated icosahedron (20 regular hexagons) and the chamfered dodecahedron (30 mirror-symmetric hexagons). Here are three other examples:

60 mirror-symmetric hexagons

80 hexagons, among them 20 regular

120 hexagons, among them 60 irregular

with "rings" of squares...

If we insert three rings of four squares along the edges of a regular octahedron (12 squares and the 6 square intersections) we get the small rhombicuboctahedron.

We can insert a ring of six squares along each of the four "hexagonal equators" of the cuboctahedron (faces in dark blue).
With one ring we get the Johnson's solid J36.
With the four "rings" we have 24 squares and 12 rhombi (faces of a rhombic dodecahedron) at the intersections, that is (6+8)+24+12=50 faces.

Likewise the icosidodecahedron (faces in dark blue) has six "decagonal equators".
With one ring of ten squares we get another Johnson's solid: J43.
Three "rings" can be arranged in two different ways to form two nice polyhedra, one flat and the other stretched.
With the six "rings" we have 60 squares and 30 rhombi (faces of a rhombic triacontahedron) at the intersections, that is (20+12)+60+30=122 faces.

two rhombicosidodecahedra with golden rectangles (Ulrich Mikloweit)

 These two polyhedra stem from the small rhombicosidodecahedron in which the 30 squares have been replaced with golden rectangles. There are two ways to arrange the rectangles; with rectangles of same size we thus get two different polyhedra (on the two solids the 20 triangles and the 12 pentagons have different sizes).
The presence of triangles along two opposite sides of each rectangle creates an optical illusion; the 2×30 rectangles are identical.

a tetragonal disphenoid (noble polyhedron)

A noble polyhedron is one which is isohedral (all faces are identical) and isogonal (all vertices are identical). The dual of a noble polyhedron is also noble.

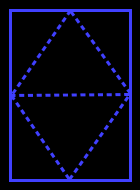
A disphenoid is an equifacial tetrahedron (four identical faces); the faces of a tetragonal disphenoid are isosceles and arranged in such a way that they create a double wedge (sphenoid comes from the Greek word for wedge).

The faces of this tetragonal disphenoid have side's lengths a√3, a√3 and 2a. Its net can be obtained by simply folding a format A sheet (2a × 2a√2). It fills the space.

disphénoïde tétragonal

an "elementary" pentahedron

This curious pentahedron is a tectohedron of order 4 (tetrahedron with a vertex cut off).
With its "mirror image" they can be used as bricks to build the five Fedorov's parallelohedra; thus they fill the space according to at least five differents assemblings.

The net is an assembling of rectangular triangles (the three quadrilaterals are inscribed in circles centered at the midpoints of their large diagonals).
To get the mirror image it suffices to turn the net over and to fold it upside down. 		patron

an unusual polyhedron

 Non trivial polyhedra with heptagonal faces are seldom seen; this one, constructed by Marcel Tünnissen, has full tetrahedral symmetry.
Its faces are all equilateral (edges of same length): 12 heptagons and 16 triangles.

Kirkman's icosahedron

 With 8 pentagons and 12 triangles, this icosahedron has outstanding properties:
  • the coordinates of its vertices are "small" integers,
  • the lengths of its edges are integers, and curiously its volume too,
  • it is auto-dual and its edges are tangent to a sphere (mid-sphere), ...
 
  (details and more surprising properties in A polyhedron full of surprises  by Hans L. Fetter)

polyhedra with near regular faces

These polyhedra are not Johnson's polyhedra because the dark blue faces are only "almost" regular.


a cube embedded in an icosahedron
(Jim McNeill)


a "fullerene" with 4 hexagons and 12 pentagons
tetrahedral symmetry (Robert Austin & Roger Kaufman)


a wedge
(Robert Webb & Alex Doskey)


More examples on an other page.

home page
French 		convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects April 1999
updated 08-03-2014