name (with link to popup applet)
image
face's colors: f3 f4 f5 f6 f8 f10 |
square pyramid
 |
pentagonal pyramid
 |
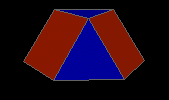
triangular cupola
| J03 |
4f3 3f4 1f6 - 6v3 3v4 |
 |
square cupola
| J04 |
4f3 5f4 1f8 - 8v3 4v4 |
 |
pentagonal cupola
| J05 |
5f3 5f4 1f5 1f10 - 10v3 5v4 |
 |
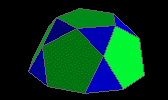
pentagonal rotunda
| J06 |
10f3 6f5 1f10 - 10v3 10v4 |
 |
elongated triangular pyramid
 |
elongated square pyramid
 |
elongated pentagonal pyramid
| J09 |
5f3 5f4 1f5 - 5v3 5v4 1v5 |
 |
gyroelongated square pyramid
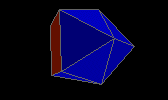 |
gyroelongated pentagonal pyramid
 |
triangular dipyramid
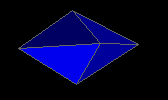 |
pentagonal dipyramid
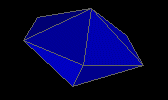 |
elongated triangular dipyramid
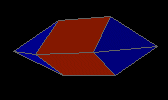 |
elongated square dipyramid
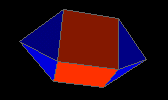 |
elongated pentagonal dipyramid
 |
gyroelongated square dipyramid
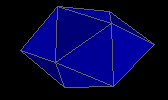 |
elongated triangular cupola
| J18 |
4f3 9f4 1f6 - 6v3 9v4 |
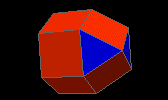 |
elongated square cupola
| J19 |
4f3 13f4 1f8 - 8v3 12v4 |
 |
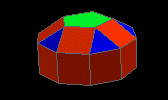
elongated pentagonal cupola
| J20 |
5f3 15f4 1f5 1f10 - 10v3 15v4 |
 |
elongated pentagonal rotunda
| J21 |
10f3 10f4 6f5 1f10 - 10v3 20v4 |
 |
gyroelongated triangular cupola
| J22 |
16f3 3f4 1f6 - 9v4 6v5 |
 |
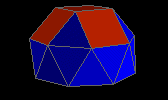
gyroelongated square cupola
| J23 |
20f3 5f4 1f8 - 12v4 8v5 |
 |
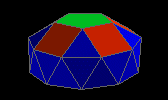
gyroelongated pentagonal cupola
| J24 |
25f3 5f4 1f5 1f10 - 15v4 10v5 |
 |
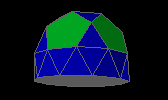
gyroelongated pentagonal rotunda
| J25 |
25f3 5f4 1f5 1f10 - 15v4 10v5 |
 |
triangular gyrobiprism
 |
triangular orthobicupola
 |
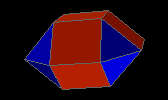
square orthobicupola
 |
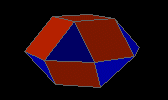
square gyrobicupola
 |
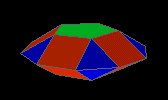
pentagonal orthobicupola
 |
pentagonal gyrobicupola
 |
pentagonal orthocupolarotunda
 |
pentagonal gyrocupolarotunda
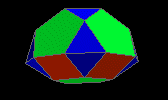 |
pentagonal orthobirotunda
 |
elongated triangular orthobicupola
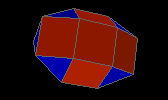 |
elongated triangular gyrobicupola
 |
elongated square gyrobicupola
 |
elongated pentagonal orthobicupola
 |
elongated pentagonal gyrobicupola
 |
elongated pentag. orthocupolarotunda
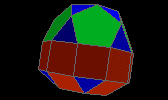 |
elongated pentag. gyrocupolarotunda
 |
elongated pentagonal orthobirotunda
| J42 |
20f3 10f4 12f5 - 40v4 |
 |
elongated pentagonal gyrobirotunda
| J43 |
20f3 10f4 12f5 - 40v4 |
 |
gyroelongated triangular bicupola
 |
gyroelongated square bicupola
 |
gyroelongated pentagonal bicupola
| J46 |
30f3 10f4 2f5 - 10v4 20v5 |
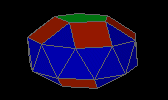 |
gyroelongated pentag. cupolarotunda
| J47 |
35f3 5f4 7f5 - 15v4 20v5 |
 |
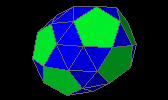
gyroelongated pentag. birotunda
| J48 |
40f3 12f5 - 20v4 20v5 |
 |
augmented triangular prism
 |
biaugmented triangular prism
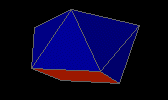 |
triaugmented triangular prism
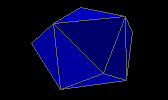 |
augmented pentagonal prism
| J52 |
4f3 4f4 2f5 - 6v3 5v4 |
 |
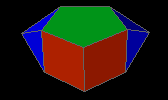
biaugmented pentagonal prism
| J53 |
8f3 3f4 2f5 - 2v3 10v4 |
 |
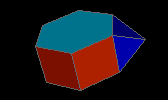
augmented hexagonal prism
| J54 |
4f3 5f4 2f6 - 8v3 5v4 |
 |
parabiaugmented hexagonal prism
| J55 |
8f3 4f4 2f6 - 4v3 10v4 |
 |
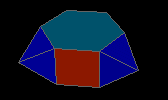
metabiaugmented hexagonal prism
| J56 |
8f3 4f4 2f6 - 4v3 10v4 |
 |
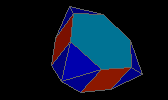
triaugmented hexagonal prism
 |
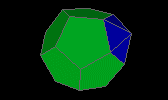
augmented dodecahedron
| J58 |
5f3 11f5 - 15v3 5v4 1v5 |
 |
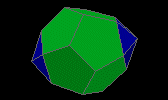
parabiaugmented dodecahedron
| J59 |
10f3 10f5 - 10v3 10v4 2v5 |
 |
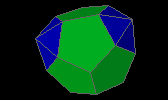
metabiaugmented dodecahedron
| J60 |
10f3 10f5 - 10v3 10v4 2v5 |
 |
triaugmented dodecahedron
| J61 |
15f3 9f5 - 5v3 15v4 3v5 |
 |
metabidiminished icosahedron
| J62 |
10f3 2f5 - 2v3 6v4 2v5 |
 |
tridiminished icosahedron
 |
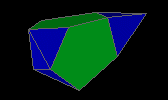
augmented tridiminished icosahedron
 |
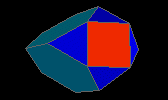
augmented truncated tetrahedron
| J65 |
8f3 3f4 3f6 - 6v3 9v4 |
 |
augmented truncated cube
| J66 |
12f3 5f4 5f8 - 16v3 12v4 |
 |
biaugmented truncated cube
| J67 |
16f3 10f4 4f8 - 8v3 24v4 |
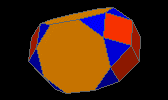 |
augmented truncated dodecahedron
| J68 |
25f3 5f4 1f5 11f10 - 50v3 15v4 |
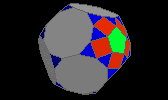 |
parabiaugmented trunc. dodecahedron
| J69 |
30f3 10f4 2f5 10f10 - 40v3 30v4 |
 |
metabiaugmented trunc. dodecahedron
| J70 |
30f3 10f4 2f5 10f10 - 40v3 30v4 |
 |
triaugmented trunc. dodecahedron
| J71 |
35f3 15f4 3f5 9f10 - 30v3 45v4 |
 |
gyrate rhombicosidodecahedron
| J72 |
20f3 30f4 12f5 - 60v4 |
 |
parabigyrate rhombicosidodecahedron
| J73 |
20f3 30f4 12f5 - 60v4 |
 |
metabigyrate rhombicosidodec.
| J74 |
20f3 30f4 12f5 - 60v4 |
 |
trigyrate rhombicosidodecahedron
| J75 |
20f3 30f4 12f5 - 60v4 |
 |
diminished rhombicosidodecahedron
| J76 |
15f3 25f4 11f5 1f10 - 10v3 45v4 |
 |
paragyrate dimin. rhombicosidodec.
| J77 |
15f3 25f4 11f5 1f10 - 10v3 45v4 |
 |
metagyrate dimin. rhombicosidodec.
| J78 |
15f3 25f4 11f5 1f10 - 10v3 45v4 |
 |
bigyrate diminished rhombicosidodec.
| J79 |
15f3 25f4 11f5 1f10 - 10v3 45v4 |
 |
parabidiminished rhombicosidodec.
| J80 |
10f3 20f4 10f5 2f10 - 20v3 30v4 |
 |
metabidiminished rhombicosidodec.
| J81 |
10f3 20f4 10f5 2f10 - 20v3 30v4 |
 |
gyrate bidiminished rhombicosidodec.
| J82 |
10f3 20f4 10f5 2f10 - 20v3 30v4 |
 |
tridiminished rhombicosidodecahedron
| J83 |
5f3 15f4 9f5 3f10 - 30v3 15v4 |
 |
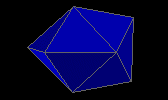
snub disphenoid
 |
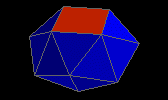
snub square antiprism
 |
sphenocorona
 |
augmented sphenocorona
 |
sphenomegacorona
 |
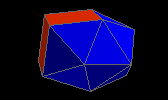
hebesphenomegacorona
 |
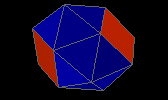
disphenocingulum
 |
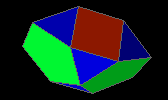
bilunabirotunda
| J91 |
8f3 2f4 4f5 - 4v3 10v4 |
 |
triangular hebesphenorotunda
| J92 |
13f3 3f4 3f5 1f6 - 18v4 |
 |




























































































