Curiosité : en alternant ce polyèdre avec un dodécaèdre régulier on peut remplir l'espace.

Il a une symétrie tétraédrique sans plan de réflexion, donc existe en deux versions images dans un miroir.
|
composé de deux prismes triangulaires
|
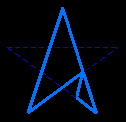
pyramide régulière pentagrammique
|
prisme régulier pentagrammique
|
une étoile pentagonale
|
bipyramide pentagrammique
|
antiprisme régulier pentagrammique non croisé
|
| Ce polyèdre uniforme, le tétrahémihexaèdre, n'a que sept faces : quatre triangles et trois carrés passant par le centre et deux à deux orthogonaux. Ses douze arêtes sont les côtés des quatre triangles. C'est une surface à un seul côté, donc non orientable.
Cet heptaèdre est un octaèdre régulier facetté ; on a excavé quatre pyramides régulières trirectangles. |
||
|
|
|
| Les faces de ce dodécaèdre sont des pentagones symétriques non convexes (partie de pentagramme) identiques. Il a une symétrie tétraédrique avec seulement trois plans de réflexion deux à deux orthogonaux.
Curiosité : en alternant ce polyèdre avec un dodécaèdre régulier on peut remplir l'espace.
|
|
| Les faces de ce dodécaèdre décrit par George Olshevsky sont aussi des pentagones non convexes identiques découpés dans un triangle d'or à angles aigus : une face est l'assemblage de deux triangles d'or à angle obtus (un sommet du pentagone appartient au côté opposé).
Il a une symétrie tétraédrique sans plan de réflexion, donc existe en deux versions images dans un miroir.
|
|
|
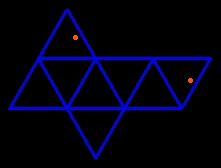
Le patron de ce deltaèdre non convexe est aussi un patron de l'octaèdre régulier ; cela signifie que les deux polyèdres ont les mêmes faces, mais l'un est convexe et l'autre ne l'est pas. Les deux côtés marqués d'un point rouge forment l'arête de l'unique "pli vallée". |
 |
|
symétrie tétraédrique (6 plans de symétrie, 24 faces) |
symétrie octaédrique (9 plans de symétrie, 48 faces) |
|
7x(2x5) = 70 faces |
3x(2x5) + 3x(2x4) = 54 faces |
|
3 triangles, 3 carrés et 3 pentagones |
un toroïde avec 6 triangles et 6 pentagones |
|
|
|
Sur les deux composés l'intersection des trois prismes est un cube ; taper "f" pour voir ce cube caché.
| références : |
• http://cs.stmarys.ca/~dawson/images3.html par Robert Dawson (en anglais).
• Hedron par Jim McNeill |
page accueil
 |
polyèdres convexes - polyèdres non convexes - polyèdres intéressants - sujets connexes | janvier 2001 mis à jour 08-08-2012 |